Design of Multishell Sampling Schemes with Uniform Coverage in Diffusion MRI

Emmanuel Caruyer; Christophe Lenglet; Guillermo Sapiro; Rachid Deriche

doi:10.1002/mrm.24736

. Author manuscript; available in PMC: 2017 Apr 5.

Published in final edited form as: Magn Reson Med. 2013 Apr 26;69(6):1534–1540. doi: 10.1002/mrm.24736

Design of Multishell Sampling Schemes with Uniform Coverage in Diffusion MRI

Emmanuel Caruyer ^1,^*, Christophe Lenglet ², Guillermo Sapiro ^3,^†, Rachid Deriche ¹

PMCID: PMC5381389 NIHMSID: NIHMS590155 PMID: 23625329

Abstract

Purpose

In diffusion MRI, a technique known as diffusion spectrum imaging reconstructs the propagator with a discrete Fourier transform, from a Cartesian sampling of the diffusion signal. Alternatively, it is possible to directly reconstruct the orientation distribution function in q-ball imaging, providing so-called high angular resolution diffusion imaging. In between these two techniques, acquisitions on several spheres in q-space offer an interesting trade-off between the angular resolution and the radial information gathered in diffusion MRI. A careful design is central in the success of multishell acquisition and reconstruction techniques.

Methods

The design of acquisition in multishell is still an open and active field of research, however. In this work, we provide a general method to design multishell acquisition with uniform angular coverage. This method is based on a generalization of electrostatic repulsion to multishell.

Results

We evaluate the impact of our method using simulations, on the angular resolution in one and two bundles of fiber configurations. Compared to more commonly used radial sampling, we show that our method improves the angular resolution, as well as fiber crossing discrimination.

Discussion

We propose a novel method to design sampling schemes with optimal angular coverage and show the positive impact on angular resolution in diffusion MRI.

Keywords: Diffusion MRI, experiment design, q-space imaging

Introduction

Diffusion MRI is an imaging technique discovered in the mid 1980s (1–3) that maps the local displacement probability of water molecules within biological tissues. This has provided a great tool over the past 20 years for the early diagnosis of brain disorders and the study of brain structural connectivity, and a precious help for preoperative planning in neurosurgery (4,5). Using a pulsed-gradient spin-echo sequence (6), the MR echo magnitude is attenuated due to proton diffusion, and by repeating acquisitions with various diffusion encoding gradients, one can characterize and recover information on the water molecules displacement. This in turns reflect the organization of the underlying tissue microstructure, which restricts the displacement of water molecules.

Formally, the diffusion of water molecules is well described by the ensemble average propagator, P(r; τ), which is the full 3D probability density function of water molecules displacement during a given observation time τ. Under the narrow-pulse assumption, which is verified whenever the diffusion time τ is much larger than the pulse duration δ, the signal attenuation, E(q), is related to the ensemble average propagator through a Fourier transform (7):

E (q) \int_{R^{3}} P (r) e^{2 ı π q \cdot r} d r,

[1]

where the wavevector is q = γδG/2π, γ is the gyromagnetic ratio, and G is the magnetic field gradient.

A technique, known as q-space imaging or diffusion spectrum imaging (7,8), consists in sampling the diffusion weighted MR attenuation E(q) on a Cartesian grid in the reciprocal space. The ensemble average propagator is then reconstructed through a discrete Fourier transform, and other quantities of interest can be computed such as the orientation distribution function (ODF), ψ(u), which is the angular marginal probability density of water molecules motion. This technique has been applied successfully for the in vivo imaging of human brain white matter structures. However, the long acquisition time required for such technique limits its application in a clinical context. Several approaches (9–13) use a hybrid sampling method, where the diffusion attenuation E(q) is sampled on several spheres in the q-space, rather than on a Cartesian lattice. Multiple q-shell sampling offers an interesting trade-off between classical high angular resolution diffusion imaging techniques in q-ball imaging (14,15), and diffusion spectrum imaging.

The design of sampling protocols in single shell has received much attention from the community (16–18). However, the design of multishell sampling is still an active subject of research. There are many degrees of freedom in the construction of a multishell design. If we try to determine all the parameters that fully describe a sampling protocol on several shells, we have: the total number of samples, K; the number of spheres in the q-space, S; the shell radii (related to the b-values), q_s; the number of points on each shell, K_s, such that Σ_s_≤_S K_s = K, and the directions on each sampling shell, u_s_,_k ∈ 𝒮². With the large and increasing number of reconstruction techniques in the literature (9,10,13,19–22), it is not clear whether a preferred, unified strategy would fit the needs of every method. In particular, we believe that the selection of parameters K, S, q_s, and K_s should be driven by the needs of the reconstruction method, the time limit for the acquisition, and the physical limitations of the imaging system. Still, the choice of sampling directions should follow the same unified strategy, commonly adopted in q-ball imaging (16–18), to achieve an angular coverage as uniform as possible. As for the choice of shell radii, number of shells and number of points per shell, we will follow the strategy recently proposed in Ref. 22, which is optimized for reconstruction in the continuous and orthonormal basis called modified spherical polar Fourier (mSPF) (23).

In particular, recent studies have shown that for a better angular resolution, the sampling directions should be as different as possible from one shell to another (21,24,25). The constructions in Refs. 24 and 25 start from a uniform set of directions on the unit sphere, which is then separated into S subsets of quasi-uniform directions on the sphere, that correspond to the S spheres under consideration for sampling. This method leads to a discrete search problem, that is solved at the cost of a timely optimization procedure in Ref. 25, or at the cost of a suboptimal greedy approach in (24). Another related method, presented in Ref. 26 and, in deeper details, in a private communication with the authors, starts from independent sets of directions uniformly spread on the sphere, and then finds the optimal composition of rigid rotations of each set with respect to the others, so that the projection of the rotated sets of points onto the same unit spheres gives the most uniform coverage possible. Finally, the method in Ref. 21 is based on a geometrical construction, using the concept of uniform and dual polyhedra. The vertices of two polyhedra dual to each other give two complementary sets of directions, that are used to design multishell sampling strategy. The drawback with this technique is that it only provides two separate sets of directions, which is not enough for more than two shells sampling. Moreover, the choice of the number of points per shell is limited by the finite number of uniform polyhedra (see Ref. 27 and the related software Kaleido for a mathematical construction).

In this work, we present a general method to design multishell sampling protocols, with a uniform coverage on each shell, and a global uniform angular coverage. We propose a cost function that generalizes electrostatic repulsion to multishell, which is presented in the first section, together with an efficient method to minimize this cost function. We also show that the same objective function can be used to design incremental acquisition schemes, which are compatible with prematurely aborted scans. In the “Results” section, we compute some geometrical properties of the optimal point sets. We demonstrate the properties of our new sampling scheme through Monte-Carlo simulations. A preliminary version of this work was presented in Refs. 28 and 29.

Methods

The cost function we present in this section is a generalization of the electrostatic repulsion in high angular resolution diffusion imaging (16–18), adapted to the problem of multishell sampling. The cost function is made of two terms: the first term controls the repartition on each shell, whereas the second controls the angular uniformity of the set of directions as a whole. A point set minimizing this cost function can be constructed by direct minimization, and we report how to minimize this cost function. Alternatively, to construct incremental acquisition schemes, that are compatible with prematurely stopped scans (see Ref. 30 for instance in q-ball imaging), the same cost function can be minimized incrementally, following the method in Ref. 31.

Multishell q-Space Sampling with Uniform Coverage

In the design of q-ball imaging acquisition, the most popular approach is to spread out the sampling directions as uniformly as possible on the sphere (16–18). Similarly, we propose to construct the sampling directions on each shell, with the following principles: First, for the sake of rotational invariance, it is desirable that the coverage of each sphere be as uniform as possible. Second, we require the whole set of directions (i.e., the set of all sampling points in q-space, reprojected onto the unit sphere) to be as uniform as possible. We, therefore, propose a split cost function V = αV₁ + (1 − α)V₂, where V₁ and V₂ address, respectively, the two principles stated earlier.

The cost function, is a natural generalization of the method in Refs. 16 and 18 to multishell,

V_{1} = \frac{1}{S} \sum_{s = 1}^{S} \frac{1}{K_{s}^{2}} \sum_{i < j} v (u_{s, i}, u_{s, j}),

[2]

where S is the number of shells, K_s is the number of points on shell s, and {u_s_,_k, k = 1 … K_s} are the unit directions on shell s. The magnitude of the elementary electrostatic repulsion force, v, between two points u and v on the unit sphere is “according to Coulomb's law, inversely proportional to the square of the distance between the charges” (see Ref. 16),

v (u, v) = \frac{1}{{‖ u - v ‖}^{2}} + \frac{1}{{‖ u + v ‖}^{2}} .

[3]

This elementary repulsion force ensures that a sampling direction, u, and its opposite −u play the same role (16,32). Minimizing the cost function V₁ corresponds to minimizing the electrostatic cost function on each shell, separately. Note that the cost of shell s is weighted by $1 / K_{s}^{2}$ ; indeed, the cost function increases as K² (32), and this weighting ensures equal importance of the uniformity for each shell.

So that the whole set of sampling directions be uniform, we also consider this second cost function

V_{2} = \frac{1}{K^{2}} \sum_{s \neq t} \sum_{i = 1}^{K_{s}} \sum_{j = 1}^{K_{t}} v (u_{s, i}, u_{t, j}),

[4]

where K is the total number of sampling points in q-space. This cost function, V₂, is the sum of magnitude of all electrostatic forces between any two directions coming from two different shells. This will ensure that the optimal directions are different from one shell to another.

Finally, we construct our set of points by minimizing the cost function

V = α V_{1} + (1 - α) V_{2},

[5]

under the constraint that each direction lies on the unit sphere,

arg min_{u_{s, k} \in R^{3}} V (u_{s, k}), subject to \forall s \in {1 \dots S}, \forall k \in {1 \dots K_{s}}, {‖ u_{k, s} ‖}^{2} = 1 .

[6]

This minimization is a nonconvex optimization problem under quadratic equality constraint. We implemented the minimization through sequential least squares quadratic programming, with analytically precalculated gradient to speedup the optimization. The gradient of the functional V is derived from the partial derivatives of v(u, v),

\frac{\partial v}{\partial x_{u}} = - 2 (\frac{x_{u} - x_{v}}{{‖ u - v ‖}^{4}} + \frac{x_{u} + x_{v}}{{‖ u + v ‖}^{4}}),

[7]

where the directions are parameterized by their Cartesian coordinates, u = [x_u y_u z_u]^T. Besides, the equality constraint is also easily implemented, as the normal to the surface defined by the equality constraint is known: it is simply u_s_,_k. Our implementation, in Python™, makes use of the fmin_slsqp routine from the SciPy optimization package (33). An example of optimal configuration on three shells, with 30 points per shell, and a weighting parameter α = 0.5 is plotted on Figure 1.

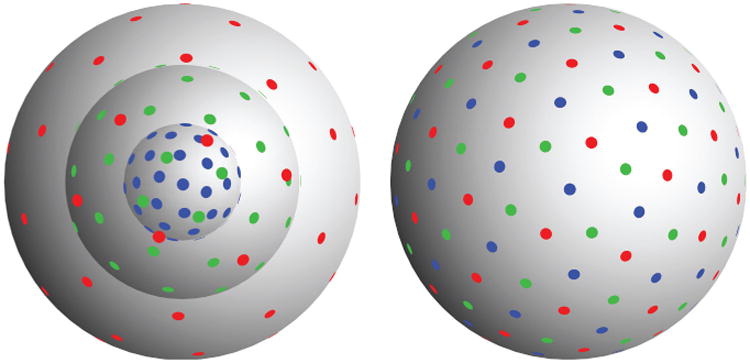
Fig. 1 — Optimal point set on three shells, 30 points per shell. The weighting parameter is set to α = 0.5. (Left) sample points in the q-space, (right) sampling directions, i.e., the sampling points reprojected onto the unit sphere.

The weighting parameter α ∈ [0, 1] balances the trade-off between uniformity on each shell (measured by cost function V₁), and angular uniformity of the sampling scheme as a whole (measured by function V₂). The case α = 0 is somehow underdetermined, as any rotation of one shell with respect to the others does not change the cost function. At the opposite, the case α = 1 would put all the weight on the global angular uniformity, but nothing would prevent poor coverage of each single shell. These two extremal cases are illustrated in Figure 2.

Fig. 2 — Extremal values of the weighting factor α: minimum cost configurations for S = 2 shells, K₁ = K₂ = 50 points per shell, points reprojected on the unit sphere. (Left) α = 0: all the importance is given to the uniformity of the configuration on each shell, independently of the other. As a result, the global coverage is nonuniform, and so we get almost “aligned” sampling on both shells. (Right) α = 1: the global angular coverage is uniform, but if we consider the repartition of points on shell 1 (green dots) or shell 2 (red dots) separately, the angular coverage is not uniform.

We plot in Figure 3 the value of both energies V₁ and V₂ for the configuration minimizing V, while the α parameter varies from 0 to 1. Except near these extremal values of α, the solution is not much sensitive to the choice of α. We chose α = 0.5 throughout our experiments.

Fig. 3 — (Left) Cost function V₁, measuring uniformity on each shell, and (right) V₂, measuring uniformity of the set of directions as a whole. Cost function evaluated for the optimum configurations, for various α. Except near 0 and 1, the solution does not depend strongly on the choice of α. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Incremental Construction of an Optimal Arrangement

Some recent work on single shell acquisition design (30–32) have shown the practical interest of incrementally optimal sampling sequences. In short, these acquisition sequences are carefully designed and ordered, so that an interruption at any point of the acquisition would result in an approximately optimal design. Such designs are compatible with acquisitions that have been stopped early because of subject motion or request. In q-ball imaging, the greedy optimization method proposed in Ref. 31 was shown to be very computationally attractive. Besides, in q-ball imaging, point sets generated with this method well compare to results obtained by a modification of the cost function, introducing weighting in the sum of magnitude of electrostatic elementary repulsion forces, as in Refs. 30 and 32. For these reasons, we adapt the approach in Ref. 31 to the problem of multishell design.

To find a nearly optimal design for K points, we construct the point set incrementally. At each iteration k, we first select the sphere s_k on which to add the kth point, so that the ratio of samples on each shell is approximately respected. Then we find the direction u minimizing V, while the k – 1 previously defined directions remain fixed. This minimization algorithm is very efficient, as at each step, we need to optimize a single direction (two parameters). Furthermore, as we show in the “Results” section, the geometrical properties of this incrementally constructed point set are close to the optimal one, provided that enough sample points are considered.

Results

Geometrical Properties of Multishell Point Sets

We present in this section some geometrical measures on the generated point sets and compare to optimal configurations on the sphere. We also compare the incremental point sets configurations to the optimal configurations. As a measure of the uniformity of a set of directions 𝒳 = {u_k, k ∈ 𝒦}, we compute the minimum angular distance between any two points, defined as

d (X) = min_{i \neq j} arccos (| u_{i} \cdot u_{j} |) .

The larger d(𝒳), the more uniform is the set of directions 𝒳. For reference, we compare to the minimum angular distance of the optimal electrostatic distribution with the same number of points.

We generated sampling protocols on S = 2–4 shells, with the same number of points per shell. The total number of points ranges from K = 12–240. We report in Figure 4 (left) the minimum angular distance between any two points on the same shell. Similarly, we report the minimum angular distance between any two points of the whole set of points, in Figure 4 (right). The minimum angular distance remains close to that of the optimal point sets with same number of points, which suggests that the method offers a very good compromise between uniformity per shell, and global uniformity. This means there is very little price to pay on the uniformity per shell, to get a globally angular uniform configuration. This validate our approach, which consists in optimizing both the angular distribution of the sampling protocol and the distribution on each single shell.

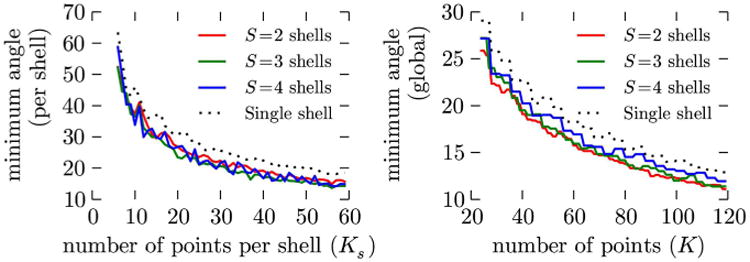
Fig. 4 — Minimum angular distance (◦) between any two points (left) within the same shell and (right) globally. We compare the sets generated using generalized electrostatic analogy, for S = 2–4 shells, to the optimum electrostatic point sets in one shell. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

We also evaluate the geometrical properties of incrementally constructed multishell point sets. We report in Figure 5 the minimum angular distance between any two points, per shell and as a whole. We observe that, provided that enough measurements are considered, the values of the minimum angular distance are reasonably close to that of the optimal configuration on a single shell, for the same number of points.

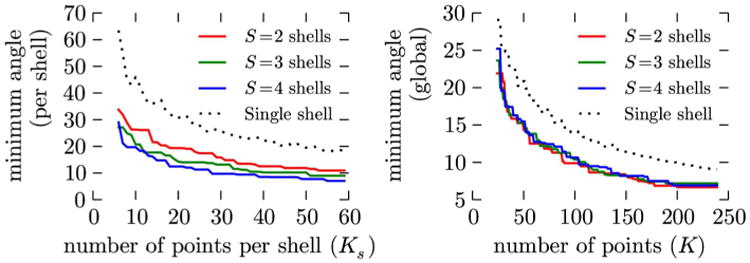
Fig. 5 — Geometrical properties of the incrementally constructed point sets on S shells. Minimum angular distance (◦) between any two points (left) within the same shell and (right) globally. We compare the incremental sets generated using generalized electrostatic analogy, for S = 2–4 shells, to the optimum electrostatic point sets in one shell. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Finally, we compare our method to three other state-of-the-art approaches that were briefly presented in the “Introduction,” and aim at constructing acquisition designs on multiple shells with uniform angular coverage. The first method, called sparse and optimal acquisition (SOA) designs (25), starts from a uniform arrangement of K points on the unit sphere. Then, it searches for the optimal partition of this set of points into S subsets (corresponding to S spheres), with K_s points on shell s, with respect to an objective function. We use the Java implementation provided in the HI-SPEED software, publicly available on the first author's website. The second method (24) also starts from a set of K points uniformly spread on the unit sphere, though obtained with a different method (34). Then it constructs S subsets which are nearly optimal, minimizing electrostatic energy in a greedy fashion (35). We will refer to this method as discrete greedy. The last method was presented in Ref. 26 and, in deeper details, in a private communication with the authors. This method starts from S independent sets of directions uniformly spread on the sphere and then finds the optimal composition of rigid rotations of each set with respect to the others, so that the projection of the rotated sets of points onto the same unit spheres gives the most uniform coverage possible. We will refer to this last method as solid rotation optimization. The optimization is done using simulated annealing, and implemented in Python™, with the anneal routine from the SciPy optimization package (33). The minimum angular distance per shell and globally are compared and reported in Table 1.

Table 1.

Minimum Angular Distance for a Three-Shell Design, with Equal Number of Points per Shell K_s = 28.

	Shell 1 K₁ = 28(°)	Shell 2 K₂ = 28(°)	Shell 3 K₃ = 28(°)	Global K = 84(°)
SOA design (25)	15.9	15.8	16.7	15.1
Discrete greedy (24)	14.5	14.5	14.5	0.0
Solid rotation (26)	25.7	25.7	25.7	7.4
Generalized electrostatic (this article)	22.2	22.2	22.0	13.2
Single shell (for reference) (16,18)	25.7	25.7	25.7	15.6

Open in a new tab

On the last row, we also report the minimum angular distance of the optimal single shell point set with the same number of points (28 points for the first three rows and 84 for the last row).

Minimization of the Cost Function

As already stated earlier, the minimization of cost function V is a nonconvex optimization problem, and we have no mathematical clue on the convergence of the optimization. We decided to test this point by repeating the optimization process, with random initial guess. The difference observed in the cost function at the end of the optimization is of the order of 10⁻², which is negligible.

Another concern is about the computational cost of the minimization. While we cannot precisely measure the implementation of the SOA method (25), as the HI-SPEED software packages come with a GUI, we observed a time of several hours for the computation of a point set with 100 points on a modern desktop computer. Our method, the solid rotation method (26) and the discrete greedy method (24) give a result within minutes on the same hardware, and therefore are more attractive from a computational perspective.

Monte-Carlo Simulations

We provide in this section an experimental validation of our sampling approach. We test the sampling schemes and evaluate the angular resolution of generalized electrostatic, compared to the other, above-mentioned approaches.

We simulated a single fiber by a cylinder with impermeable wall. The diffusion signal was simulated following (36). The cylinder dimensions were set to L = 5 mm, and ρ = 5 μm; and the diffusion time is set to τ = 20.8 ms. The signal is simulated for different acquisitions schemes, with a maximum wavevector norm q_max = 60 mm⁻¹, which corresponds to a b value b_max = 3000smm⁻². The diffusion weighted signal was corrupted by Rician noise, with corresponding SNR = 25 with respect to the baseline, nondiffusion-weighted signal. This corresponds to a SNR range from 0.1 to 7.0 on the diffusion-weighted signal.

From these noisy measurements, we fit a diffusion tensor model, using the weighted linear least squares method (37). This process is repeated 100 times for a given cylinder model, to get an estimate of the average angular error. To test the rotational invariance of acquisition schemes, this in turn is repeated 2000 times, for cylinders with different axis orientations. Acquisition protocols are defined on S = 3 shells in q-space, where the shell radii q₁–q₃ are evenly distributed between q_min and q_max. The number of points per shell is the same on each shell K_s = 8, which corresponds to a total of K = 24 measurements, typical in diffusion tensor imaging. For reference, we also compare to a single shell experiment with K = 24 measurements, q = q_max. Results are reported in Figure 6. and in Table 2.

Fig. 6 — Average angular error between the principal direction of the estimated tensor and the axis of the cylinder. Signal simulation and reconstruction were repeated with 2000 different cylinder orientations following a random uniform distribution on the sphere, and 100 repetitions with random, Rician noise for each orientation. We plot here the median, first and third quartiles, and extremal values of the angular error (in degrees). The height of each boxplot represents how rotationally invariant each method performs. See Table 2 for quantitative results. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 2.

Angular Error Between the Principal Direction of the Estimated Tensor and the Axis of the Cylinder.

	Radial	Single shell	Generalized electrostatic	SOA	Solid rotation	Discrete greedy
Angular error	2.70°±0.22	2.71°±0.09	2.44°±0.10	2.44°±0.10	2.47°±0.11	2.88°±0.34

Open in a new tab

We report the median and angular deviation. See Figure 6 for more details.

We also compare the accuracy of multiple fiber detection and discrimination. The signal is now simulated using a mixture of two Gaussian distributions, with equal compartment size,

E (q) = 0.5 (exp (- q^{T} D_{1} q) + exp (- q^{T} D_{2} q))) .

[8]

The corresponding diffusion tensors D₁ and D₂ have a FA = 0.7 and a mean diffusivity 2.1 × 10⁻³ m · ms⁻¹. This corresponds to classical values for the apparent diffusion tensor observed in brain white matter. We consider a 60° crossing angle. The signal is corrupted by Rician noise, with corresponding SNR = 25 with respect to the baseline, nondiffusion-weighted signal. This corresponds to a SNR range from 1.0 to 20.0 on the diffusion-weighted signal.

The signal is estimated in the continuous, mSPF basis with Laplace regularization (23). This is an orthonormal basis of continuous functions to represent the diffusion signal. The coefficients of the signal are estimated analytically, with a Laplace regularization penalty to promote smoothness. From the coefficients of the signal in this basis, the ODF in constant solid angle is estimated analytically using the SPFI method in Ref. 38. The angular and radial truncation orders were set to L = 6 and N = 2, respectively. The maxima of the ODF are computed with a discrete search on a set of 10,000 points on the sphere, leading to an accuracy of 0.1°.

We compare several acquisition protocols with K = 100 points and a maximum b-value of 2500 s mm⁻². For radial sampling, discrete greedy sampling (24) and solid rotation sampling (26), we use four shells with radii linearly spaced between q_min and q_max, and K_s = 25 points per shell. For the SOA design, we use 10 shells, each with K_s = 10 points per shell, as advocated in Ref. 25. Finally, for the generalized electrostatic, we use the sampling strategy proposed in Ref. 22 and optimized for reconstruction in mSPF with radial truncation order N = 2. This corresponds to a design on S = 2 shells, with b-values 900 and 2500 s mm⁻², and K₁ = 24, k₂ = 76 points per shell, respectively. Results of the reconstructed crossing angle are reported on Figure 7 and in Table 3. As for the previous experiments, the simulation was repeated 1000 times, with Rician noise and random rotation of the fibers to test the rotational invariance of the reconstruction.

Fig. 7 — Crossing angle for a reconstructed fiber crossing. The q-space signal was reconstruction in the mSPF basis, with Laplace regularization (see Ref. 23), fixed regularization weight λ = 0.5. The ODF was further estimated using the SPFI method in Ref. 38. The boxplot represents min and max values, as well as the first and third quartiles. We also compare to the ODF reconstructed in constant solid angle (19), for a single shell experiment with the same number of points K = 100. See also Table 3. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 3.

Crossing Angle for a Reconstructed Fiber Crossing (Ground Truth is 60°).

	Radial	CSA ODF	Generalized electrostatic	SOA	Solid rotation	Discrete greedy
Estimated crossing	58.5°±3.8	66.1°±2.6	61.5°±2.7	59.4°±4.0	59.2°±3.5	59.2°±3.7

Open in a new tab

See legend in Figure 7 for more details.

While for the reconstruction of a single fiber, either method give comparable results, the reconstruction with our method gives the lowest dispersion in angle estimation, and a very small bias, when it comes to multiple shell detection.

Discussion

We have proposed a novel, efficient method to generate sampling schemes for multishell acquisitions. Our method is dedicated to the placement of acquisition directions on each sphere, with a good angular distribution per shell and as a whole. The cost function we propose is an extension of the electrostatic repulsion to multishell. With an adequate minimization algorithm, we show that this cost function can be used to create acquisition with incremental angular distribution, that is compatible with prematurely stopped scans.

The focus of the study is more on the angular distribution of points. As for the choice of number of shells, shell radii, number of points per shell, we suggest to follow the strategy optimized for reconstruction in mSPF, recently presented in Ref. 22.

The geometrical properties of the generated point sets are satisfactory: the angular distribution per shell is indeed very close to the optimal arrangements in q-ball imaging. This is also the case for the angular distribution as a whole. The compromise between the global angular distribution and the angular distribution on each shell is better than for the other methods to which we compared: we are able to increase the global uniformity, at a very small cost on the uniformity on each shell. In simulations, for the reconstruction of single and multiple fiber compartments, this sampling strategies gives a better angular precision than prior arts methods. Single fiber orientation is determined with a lower angular error than simply radial sampling, and the crossing angle in two fibers case is also more accurate.

Acknowledgments

This work was partly supported by Inria CD-MRI Associate Team program, ANR NucleiPark, France-Parkinson Foundation, and NIH Grants P41 RR008079 (NCRR), P41 EB015894 (NIBIB), P30 NS057091, and P30 NS076408. C. Lenglet and G. Sapiro were partly supported by the NIH Human Connectome Project U54 MH091657 and Grant R01 EB008432. G. Sapiro received additional support from ONR, NGA, NSF, DARPA, NSSEFF, and ARO. The authors thank the authors of SOA design method (25) for their publicly available implementation, in the HI-SPEED software (https://sites.google.com/site/hispeedpackets).

References

1.Le Bihan D, Breton E. Imagerie De diffusion it in vivo par rsonnance magntique nuclaire. CR Acad Sci. 1985;301:1109–1112. [Google Scholar]
2.Taylor D, Bushell M. The spatial mapping of translational diffusion coefficients by the NMR imaging technique. Phys Med Biol. 1985;30:345–349. doi: 10.1088/0031-9155/30/4/009. [DOI] [PubMed] [Google Scholar]
3.Merboldt K, Hanicke W, Frahm J. Self-diffusion NMR imaging using stimulated echoes. J Magn Reson. 1985;64:479–486. [Google Scholar]
4.Jones DK, editor. Diffusion MRI: theory, methods, and applications. New York: Oxford University Press; 2010. [Google Scholar]
5.Johansen-Berg H, Behrens TE, editors. Diffusion MRI: from quantitative measurement to in-vivo neuroanatomy. London: Academic Press; 2009. [Google Scholar]
6.Stejskal E, Tanner J. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965;42:288–292. [Google Scholar]
7.Callaghan PT. Principles of nuclear magnetic resonance microscopy. Oxford: Clarendon; 1991. [Google Scholar]
8.Wedeen V, Hagmann P, Tseng W, Reese T, Weisskoff R. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson in Med. 2005;54:1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
9.Wu Y, Alexander A. Hybrid diffusion imaging. NeuroImage. 2007;36:617–629. doi: 10.1016/j.neuroimage.2007.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Khachaturian M, Wisco J, Tuch D. Boosting the sampling efficiency of q-ball imaging using multiple wavevector fusion. Magn Reson Med. 2007;57:289–296. doi: 10.1002/mrm.21090. [DOI] [PubMed] [Google Scholar]
11.Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N. Multiple q-shell ODF reconstruction in q-ball imaging In Proceedings of the 12th International Conference on MICCAI. London: Springer; 2009. pp. 423–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Descôteaux M, Deriche R, LeBihan D, Mangin JF, Poupon C. Lecture Notes in Computer Science. Vol. 5636. Kloster Irsee, Germany: Springer; 2009. Diffusion propagator imaging: using Laplace's equation and multiple shell acquisitions to reconstruct the diffusion propagator. In Information Processing in Medical Imaging; pp. 1–13. [DOI] [PubMed] [Google Scholar]
13.Assemlal H, Tschumperlé D, Brun L. Efficient and robust computation of pdf features from diffusion MR signal. Med Image Anal. 2009;13:715–729. doi: 10.1016/j.media.2009.06.004. [DOI] [PubMed] [Google Scholar]
14.Tuch D. Q-ball imaging. Magn Reson Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
15.Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. Regularized, fast, and robust analytical q-ball imaging. Magn Reson Med. 2007;58:497–510. doi: 10.1002/mrm.21277. [DOI] [PubMed] [Google Scholar]
16.Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42:515–525. [PubMed] [Google Scholar]
17.Papadakis NG, Murrills CD, Hall LD, Huang CL, Adrian Carpenter T. Minimal gradient encoding for robust estimation of diffusion anisotropy. Magn Reson Imaging. 2000;18:671–679. doi: 10.1016/s0730-725x(00)00151-x. [DOI] [PubMed] [Google Scholar]
18.Jansons KM, Alexander DC. Persistent angular structure: new insights fom diffusion magnetic resonance imaging data. Inverse Probl. 2003;19:1031–1046. [Google Scholar]
19.Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N. Reconstruction of the ODF in single and multiple shell q-ball imaging within constant solid angle. Magn Reson Med. 2010;64:554–566. doi: 10.1002/mrm.22365. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Descoteaux M, Deriche R, Bihan DL, Mangin JF, Poupon C. Multiple q-shell diffusion propagator imaging. Med Image Anal. 2011;15:603–621. doi: 10.1016/j.media.2010.07.001. [DOI] [PubMed] [Google Scholar]
21.Ye W, Portnoy S, Entezari A, Blackband SJ, Vemuri BC. Efficient interlaced multi-shell sampling scheme for reconstruction of diffusion propagators. IEEE Trans Med Imaging. 2012;31:1043–1050. doi: 10.1109/TMI.2012.2184551. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Caruyer E, Deriche R. CDMRI—MICCAI Workshop on Computational Diffusion MRI. Nice, France: 2012. A computational framework for experimental design in diffusion MRI. [Google Scholar]
23.Caruyer E, Deriche R. Diffusion MRI signal reconstruction with continuity constraint and optimal regularization. Med Image Anal. 2012;16:1113–1120. doi: 10.1016/j.media.2012.06.011. [DOI] [PubMed] [Google Scholar]
24.Zhan L, Leow AD, Aganj I, Lenglet C, Sapiro G, Yacoub E, Harel N, Toga AW, Thompson PM. ISBI—International Symposium on Biomedical Imaging. Chicago, IL: IEEE; 2011. Differential information content in staggered multiple shell HARDI measured by the tensor distribution function; pp. 305–309. [Google Scholar]
25.Koay C, Özarslan E, Johnson KM, Meyerand ME. Sparse and optimal acquisition design for diffusion MRI and beyond. Med Phys. 2012;39:2499–2511. doi: 10.1118/1.3700166. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.De Santis S, Assaf Y, Evans CJ, Jones DK. Proceedings of the 19th Annual Meeting of ISMRM. Montréal, Canada: 2011. Improved precision in the charmed model of white matter through sampling scheme optimization and model parsimony testing; p. 3928. [Google Scholar]
27.HarEl Z. Uniform solution for uniform polyhedra. Geometriae Dedicata. 1993;47:57–110. [Google Scholar]
28.Caruyer E, Cheng J, Lenglet C, Sapiro G, Jiang T, Deriche R. MICCAI Workshop on Computational Diffusion MRI — CDMRI'11. Toronto, Canada: 2011. Optimal design of multiple q-shells experiments for diffusion MRI. [Google Scholar]
29.Caruyer E, Lenglet C, Sapiro G, Deriche R. HBM 17th Annual Meeting. Québec, Canada: 2011. Incremental gradient table for multiple q-shells diffusion MRI. [Google Scholar]
30.Dubois J, Poupon C, Lethimonnier F, Le Bihan D. Optimized diffusion gradient orientation schemes for corrupted clinical dti data sets. Magn Reson Mater Phys Biol Med. 2005;19:134–143. doi: 10.1007/s10334-006-0036-0. [DOI] [PubMed] [Google Scholar]
31.Deriche R, Calder J, Descoteaux M. Optimal real-time q-ball imaging using regularized Kalman filtering with incremental orientation sets. Med Image Anal. 2009;13:564–579. doi: 10.1016/j.media.2009.05.008. [DOI] [PubMed] [Google Scholar]
32.Cook P, Symms M, Boulby P, Alexander D. Optimal acquisition orders of diffusion-weighted MRI measurements. J Magn Reson Imaging. 2007;25:1051–1058. doi: 10.1002/jmri.20905. [DOI] [PubMed] [Google Scholar]
33.Jones E, Oliphant T, Peterson P, et al. SciPy: Open source scientific tools for Python. 2001 [Google Scholar]
34.Wong S, Roos M. A strategy for sampling on a sphere applied to 3D selective RF pulse design. Magn Reson Med. 1994;32:778–784. doi: 10.1002/mrm.1910320614. [DOI] [PubMed] [Google Scholar]
35.Zhan L, Leow AD, Jahanshad N, et al. How does angular resolution affect diffusion imaging measures? NeuroImage. 2010;49:1357–1371. doi: 10.1016/j.neuroimage.2009.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Soderman O, Jonsson B. Restricted Diffusion in Cylindrical Geometry. J Magn Reson Ser A. 1995;117:94–97. [Google Scholar]
37.Basser PJ, Mattiello J, Le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson. 1994;103B:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
38.Cheng J, Ghosh A, Deriche R, Jiang T. Medical Image Computing and Computer-Assisted Intervention—MICCAI. Vol. 6361. Beijing, China: Springer; 2010. Model-free, regularized, fast, and robust analytical orientation distribution function estimation; pp. 648–656. Lecture Notes in Computer Science. [DOI] [PubMed] [Google Scholar]

[R1] 1.Le Bihan D, Breton E. Imagerie De diffusion it in vivo par rsonnance magntique nuclaire. CR Acad Sci. 1985;301:1109–1112. [Google Scholar]

[R2] 2.Taylor D, Bushell M. The spatial mapping of translational diffusion coefficients by the NMR imaging technique. Phys Med Biol. 1985;30:345–349. doi: 10.1088/0031-9155/30/4/009. [DOI] [PubMed] [Google Scholar]

[R3] 3.Merboldt K, Hanicke W, Frahm J. Self-diffusion NMR imaging using stimulated echoes. J Magn Reson. 1985;64:479–486. [Google Scholar]

[R4] 4.Jones DK, editor. Diffusion MRI: theory, methods, and applications. New York: Oxford University Press; 2010. [Google Scholar]

[R5] 5.Johansen-Berg H, Behrens TE, editors. Diffusion MRI: from quantitative measurement to in-vivo neuroanatomy. London: Academic Press; 2009. [Google Scholar]

[R6] 6.Stejskal E, Tanner J. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J Chem Phys. 1965;42:288–292. [Google Scholar]

[R7] 7.Callaghan PT. Principles of nuclear magnetic resonance microscopy. Oxford: Clarendon; 1991. [Google Scholar]

[R8] 8.Wedeen V, Hagmann P, Tseng W, Reese T, Weisskoff R. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson in Med. 2005;54:1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]

[R9] 9.Wu Y, Alexander A. Hybrid diffusion imaging. NeuroImage. 2007;36:617–629. doi: 10.1016/j.neuroimage.2007.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Khachaturian M, Wisco J, Tuch D. Boosting the sampling efficiency of q-ball imaging using multiple wavevector fusion. Magn Reson Med. 2007;57:289–296. doi: 10.1002/mrm.21090. [DOI] [PubMed] [Google Scholar]

[R11] 11.Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N. Multiple q-shell ODF reconstruction in q-ball imaging In Proceedings of the 12th International Conference on MICCAI. London: Springer; 2009. pp. 423–431. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] 12.Descôteaux M, Deriche R, LeBihan D, Mangin JF, Poupon C. Lecture Notes in Computer Science. Vol. 5636. Kloster Irsee, Germany: Springer; 2009. Diffusion propagator imaging: using Laplace's equation and multiple shell acquisitions to reconstruct the diffusion propagator. In Information Processing in Medical Imaging; pp. 1–13. [DOI] [PubMed] [Google Scholar]

[R13] 13.Assemlal H, Tschumperlé D, Brun L. Efficient and robust computation of pdf features from diffusion MR signal. Med Image Anal. 2009;13:715–729. doi: 10.1016/j.media.2009.06.004. [DOI] [PubMed] [Google Scholar]

[R14] 14.Tuch D. Q-ball imaging. Magn Reson Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]

[R15] 15.Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. Regularized, fast, and robust analytical q-ball imaging. Magn Reson Med. 2007;58:497–510. doi: 10.1002/mrm.21277. [DOI] [PubMed] [Google Scholar]

[R16] 16.Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999;42:515–525. [PubMed] [Google Scholar]

[R17] 17.Papadakis NG, Murrills CD, Hall LD, Huang CL, Adrian Carpenter T. Minimal gradient encoding for robust estimation of diffusion anisotropy. Magn Reson Imaging. 2000;18:671–679. doi: 10.1016/s0730-725x(00)00151-x. [DOI] [PubMed] [Google Scholar]

[R18] 18.Jansons KM, Alexander DC. Persistent angular structure: new insights fom diffusion magnetic resonance imaging data. Inverse Probl. 2003;19:1031–1046. [Google Scholar]

[R19] 19.Aganj I, Lenglet C, Sapiro G, Yacoub E, Ugurbil K, Harel N. Reconstruction of the ODF in single and multiple shell q-ball imaging within constant solid angle. Magn Reson Med. 2010;64:554–566. doi: 10.1002/mrm.22365. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] 20.Descoteaux M, Deriche R, Bihan DL, Mangin JF, Poupon C. Multiple q-shell diffusion propagator imaging. Med Image Anal. 2011;15:603–621. doi: 10.1016/j.media.2010.07.001. [DOI] [PubMed] [Google Scholar]

[R21] 21.Ye W, Portnoy S, Entezari A, Blackband SJ, Vemuri BC. Efficient interlaced multi-shell sampling scheme for reconstruction of diffusion propagators. IEEE Trans Med Imaging. 2012;31:1043–1050. doi: 10.1109/TMI.2012.2184551. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] 22.Caruyer E, Deriche R. CDMRI—MICCAI Workshop on Computational Diffusion MRI. Nice, France: 2012. A computational framework for experimental design in diffusion MRI. [Google Scholar]

[R23] 23.Caruyer E, Deriche R. Diffusion MRI signal reconstruction with continuity constraint and optimal regularization. Med Image Anal. 2012;16:1113–1120. doi: 10.1016/j.media.2012.06.011. [DOI] [PubMed] [Google Scholar]

[R24] 24.Zhan L, Leow AD, Aganj I, Lenglet C, Sapiro G, Yacoub E, Harel N, Toga AW, Thompson PM. ISBI—International Symposium on Biomedical Imaging. Chicago, IL: IEEE; 2011. Differential information content in staggered multiple shell HARDI measured by the tensor distribution function; pp. 305–309. [Google Scholar]

[R25] 25.Koay C, Özarslan E, Johnson KM, Meyerand ME. Sparse and optimal acquisition design for diffusion MRI and beyond. Med Phys. 2012;39:2499–2511. doi: 10.1118/1.3700166. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] 26.De Santis S, Assaf Y, Evans CJ, Jones DK. Proceedings of the 19th Annual Meeting of ISMRM. Montréal, Canada: 2011. Improved precision in the charmed model of white matter through sampling scheme optimization and model parsimony testing; p. 3928. [Google Scholar]

[R27] 27.HarEl Z. Uniform solution for uniform polyhedra. Geometriae Dedicata. 1993;47:57–110. [Google Scholar]

[R28] 28.Caruyer E, Cheng J, Lenglet C, Sapiro G, Jiang T, Deriche R. MICCAI Workshop on Computational Diffusion MRI — CDMRI'11. Toronto, Canada: 2011. Optimal design of multiple q-shells experiments for diffusion MRI. [Google Scholar]

[R29] 29.Caruyer E, Lenglet C, Sapiro G, Deriche R. HBM 17th Annual Meeting. Québec, Canada: 2011. Incremental gradient table for multiple q-shells diffusion MRI. [Google Scholar]

[R30] 30.Dubois J, Poupon C, Lethimonnier F, Le Bihan D. Optimized diffusion gradient orientation schemes for corrupted clinical dti data sets. Magn Reson Mater Phys Biol Med. 2005;19:134–143. doi: 10.1007/s10334-006-0036-0. [DOI] [PubMed] [Google Scholar]

[R31] 31.Deriche R, Calder J, Descoteaux M. Optimal real-time q-ball imaging using regularized Kalman filtering with incremental orientation sets. Med Image Anal. 2009;13:564–579. doi: 10.1016/j.media.2009.05.008. [DOI] [PubMed] [Google Scholar]

[R32] 32.Cook P, Symms M, Boulby P, Alexander D. Optimal acquisition orders of diffusion-weighted MRI measurements. J Magn Reson Imaging. 2007;25:1051–1058. doi: 10.1002/jmri.20905. [DOI] [PubMed] [Google Scholar]

[R33] 33.Jones E, Oliphant T, Peterson P, et al. SciPy: Open source scientific tools for Python. 2001 [Google Scholar]

[R34] 34.Wong S, Roos M. A strategy for sampling on a sphere applied to 3D selective RF pulse design. Magn Reson Med. 1994;32:778–784. doi: 10.1002/mrm.1910320614. [DOI] [PubMed] [Google Scholar]

[R35] 35.Zhan L, Leow AD, Jahanshad N, et al. How does angular resolution affect diffusion imaging measures? NeuroImage. 2010;49:1357–1371. doi: 10.1016/j.neuroimage.2009.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.Soderman O, Jonsson B. Restricted Diffusion in Cylindrical Geometry. J Magn Reson Ser A. 1995;117:94–97. [Google Scholar]

[R37] 37.Basser PJ, Mattiello J, Le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson. 1994;103B:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]

[R38] 38.Cheng J, Ghosh A, Deriche R, Jiang T. Medical Image Computing and Computer-Assisted Intervention—MICCAI. Vol. 6361. Beijing, China: Springer; 2010. Model-free, regularized, fast, and robust analytical orientation distribution function estimation; pp. 648–656. Lecture Notes in Computer Science. [DOI] [PubMed] [Google Scholar]

PERMALINK

Design of Multishell Sampling Schemes with Uniform Coverage in Diffusion MRI

Emmanuel Caruyer

Christophe Lenglet

Guillermo Sapiro

Rachid Deriche