Abstract
We review how leaky competing accumulators (LCAs) can be used to model decision making in two-alternative, forced-choice tasks, and show how they reduce to drift diffusion (DD) processes in special cases. As continuum limits of the sequential probability ratio test, DD processes are optimal in producing decisions of specified accuracy in the shortest possible time. Furthermore, the DD model can be used to derive a speed-accuracy tradeoff that optimizes reward rate for a restricted class of two alternative forced choice decision tasks. We review findings that compare human performance with this benchmark, and reveal both approximations to and deviations from optimality. We then discuss three potential sources of deviations from optimality at the psychological level – avoidance of errors, poor time estimation, and minimization of the cost of control – and review recent theoretical and empirical findings that address these possibilities. We also discuss the role of cognitive control in changing environments and in modulating exploitation and exploration. Finally, we consider physiological factors in which nonlinear dynamics may also contribute to deviations from optimality.
Keywords: Accumulator, cognitive control, costs, decision making, drift-diffusion process, exploitation, exploration, optimality, robustness, speed-accuracy tradeoff
1 Introduction
In this article we review mathematical models of simple decision-making tasks, and use these to examine the extent to which human performance approaches but also deviate from optimality in such tasks. For the sake of analytic tractability, we focus on two-alternative forced-choice (2AFC) tasks, and consider linear models that are reduced forms of more biologically realistic models. Despite these restrictions, application of the models to empirical data suggests that human performance often approaches optimality, but also reveals systematic ways in which it falls short, and suggests hypotheses about why this is so. These include biased expectations, constraints on parameter estimation, and other factors – in particular the costs of cognitive control required for optimization – that are often neglected in analyses of cognitive performance.
We begin by considering how non-linear neural network models of 2AFC decision tasks can be reduced to a simple, one dimensional linear model describing a random walk, or drift-diffusion (DD) process. Such linear models have both behavioral and biological plausibility. They have long been used to model reaction time distributions and error rates in performance on 2AFC tasks [72, 41, 57, 60, 71]. Furthermore, in studies of nonhuman primates performing such tasks, direct recordings from neurons in oculomotor regions including the lateral intraparietal area (LIP), frontal eye fields and superior colliculus have shown that firing rates in these areas evolve over the course of a decision like sample paths of a DD process, rising to a threshold prior to response initiation [65, 28, 67, 61, 58, 47, 59]. Here, we review analyses showing how DD-based models predict optimal strategies for maximizing rewards [29, 4], and describe data that test such predictions. We consider possible sources for deviations from optimality that the data reveal, describe recent findings that address these possibilities, and finally discuss broader issues in the cognitive control of decision processes.
2 Optimal performance in simple decisions
How to best characterize human decision making performance, even for tasks as simple as 2AFC, has been the subject of intense investigation and controversy. The two most commonly considered types of models are: 1) “highlevel” (low-dimensional) neural networks – often called leaky competing accumulators (LCAs) – that describe the accumulation of evidence [75]; and 2) even simpler linear models implementing DD processes [57, 60], that can be derived from LCAs in a special case.
The DD process is a continuum limit of the sequential probability ratio test [78], and for statistically stationary tasks it yields decisions of specified average accuracy in the shortest possible time [29, 4]. We use this property to derive an optimal speed-accuracy tradeoff that maximizes reward rate, and then describe experiments that reveal both approximations to and failures to optimize, prompting further analyses and experiments. Our main tool is the optimal performance curve of Fig. 1, which can be used to assess performance across conditions, tasks and even individuals, irrespective of differences in task difficulty or timing. The reader wishing to skip mathematical detail can find this described following Eq. (10), and refer back to §2.1 and §2.2 as desired.
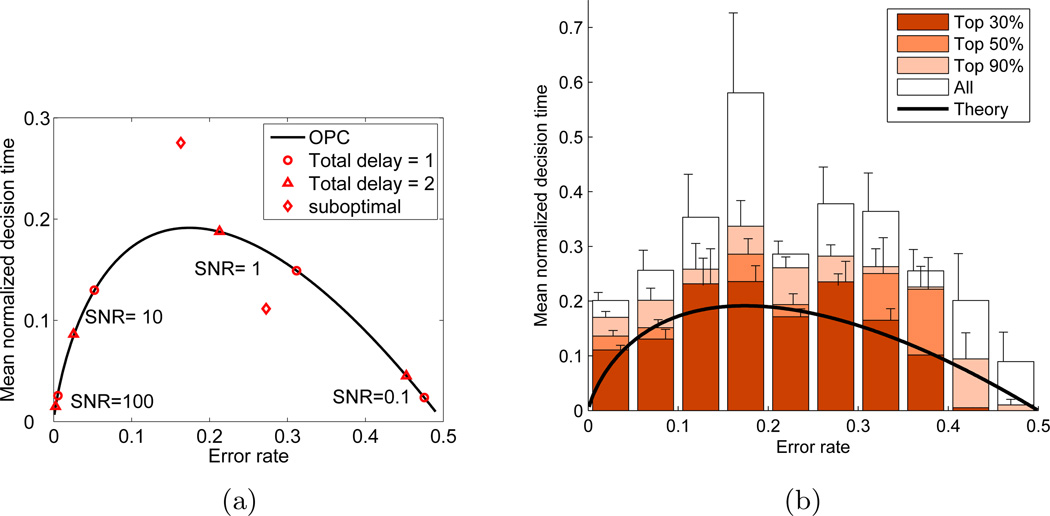
Figure 1.
(a) The optimal performance curve (OPC) of Eq. (10) relates mean normalized decision time 〈DT〉/Dtot to error-rate p(err). Triangles and circles mark hypothetical performances under 8 different task conditions; diamonds mark suboptimal performances resulting from thresholds at ±1.25 θop for SNR=1 and Dtot = 2; both reduce RR by ≈ 1.3%. (b) OPC (curve) and data from 80 human participants (boxes) sorted according to total rewards accrued over all conditions. White: all participants; lightest: lowest 10% excluded; medium: lowest 50% excluded; darkest: lowest 70% excluded. Vertical lines show SEs. From [4, 85].
2.1 Leaky competing accumulators and drift-diffusion processes
In the simplest LCA model, appropriate for 2AFC tasks, two units with activity levels (x1, x2) represent pools of neurons selectively responsive to the stimuli [75]. They mutually inhibit via input-output or frequency current (f-I) functions that express neural activity (e.g., short-term firing rates) in terms of inputs. These include constant currents representing mean stimulus levels and i.i.d. Wiener processes modeling noise that pollute the stimuli and/or enter the local circuit from other brain regions. The dynamics are governed by the following stochastic differential equations:
| (1) |
| (2) |
where the state variables xj denote unit activities (spike rates), γ, β are the leak and inhibition rates and μj, σ are the means and standard deviation of the noisy stimuli. A decision is recorded when the first activity xj(t) exceeds a fixed threshold xj,th, adjustment of which is used to tune the speed-accuracy tradeoff. Similar effects may be obtained by changing baseline activity or initial conditions, mechanisms that also appear likely, and to which we return in §3.2. See [64, 32, 75] for background on related connectionist networks, and [49] on the equivalence of different integrator models.
The function f(·) characterizing neural response is typically sigmoidal:
| (3) |
and if the gain g and bias b are set appropriately, Eqns. (1–2) without noise (σ = 0) can have one or two stable equilibria, separated by a saddle point. These correspond to two “choice attractors” in the noisy system, and if γ and β are sufficiently large, a one-dimensional, attracting curve exists that contains the three equilibria and orbits connecting them: see [24, Fig. 2] and [10]. Hence, after rapid transients have decayed following stimulus onset, the dynamics relax to that of a nonlinear Ornstein-Uhlenbeck (OU) process [10, 63]. The dominant terms are found by linearizing Eqns. (1–2) and subtracting to yield one equation for the difference x = x1 − x2:
| (4) |
In §3.5 we note that models of networks of spiking neurons can be reduced to nonlinear LCAs, providing a theoretical path from biophysical detail to analytically-tractable linear models.
Figure 2.
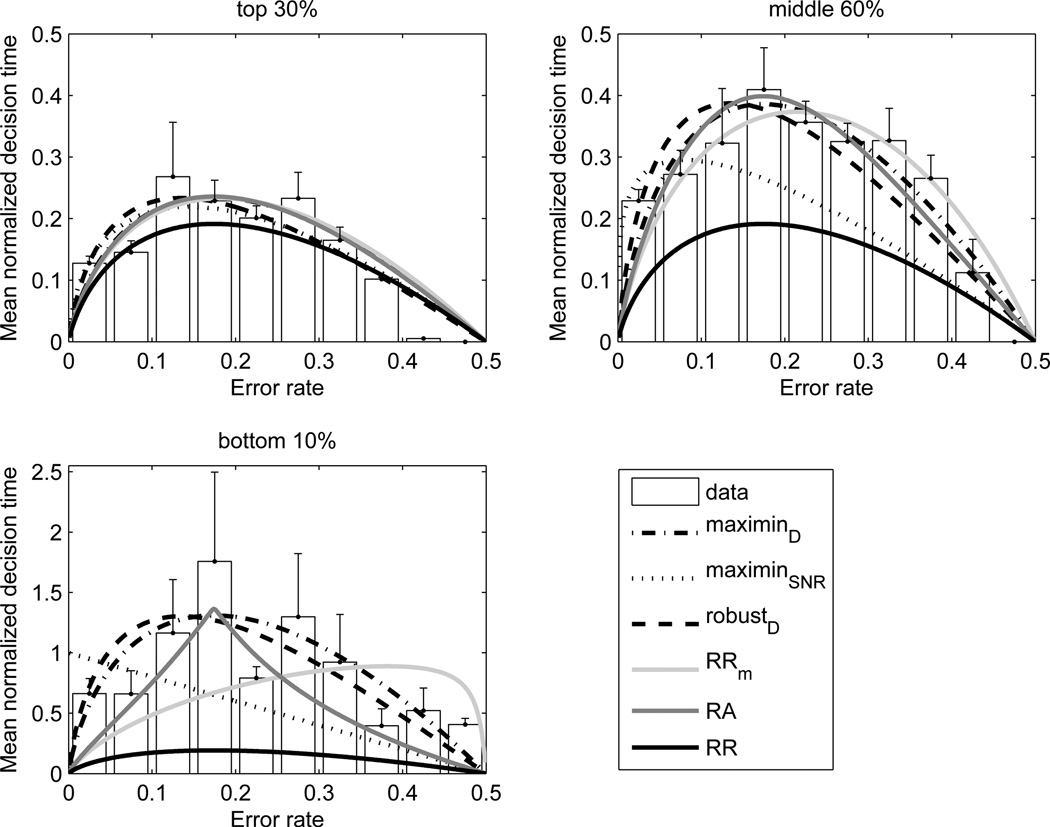
Comparisons of performance curves with mean normalized decision times (with SE bars) for three groups of participants sorted by total rewards acquired. Different curves are identified by line style and gray scale in the key, in which maximinD and maximinSNR refer to maximin performance curves (MMPCs) for uncertainty in total delay Eq. (12) and noise variance respectively, robustD to robust-satisficing performance curves (RSPCs) for uncertainty in total delay, RA and RRm denote the accuracy-weighted objective functions of Eq. (11), and RR the OPC Eq. (10). Note different vertical axis scales in upper and lower panels. From [85].
2.2 An optimal speed-accuracy tradeoff
If leak and inhibition are balanced (β = γ), and initial data are unbiased, appropriate when stimuli appear with equal probability and have equal reward value, Eq. (4) becomes a DD process
| (5) |
where A = μ1 − μ2 denotes the drift rate. Responses are given when x, identified with the logarithmic likelihood ratio, first crosses a threshold ±xth; if A > 0 then crossing of +xth corresponds to a correct response and crossing −xth to an incorrect one. The error rate and mean decision time, quantifying accuracy and speed, are
| (6) |
see [13] and [4, Appendix]. Note that the parameters A, σ and xth reduce to two quantities η ≡ (A/σ)2 (signal-to-noise ratio (SNR), having units of inverse time), and η ≡ |xth/A| (threshold-to-drift ratio, the first passage time for the noise-free process x(t) = At).
If SNR and mean response-to-stimulus interval DRSI remain constant across each block of trials, block durations are fixed, and rewards are insensitive to time, then optimality is achieved by maximising reward rate; that is, average accuracy divided by average trial duration:
| (7) |
Here T0 is that part of the reaction time due to non-decision-related (e.g., sensory and motor) processing. Since T0 and η also typically remain (approximately) constant for each participant, we may substitute Eqns. (6) into (7) and maximize RR for fixed η, T0 and DRSI, obtaining a unique threshold-to-drift ratio θ = θop for each pair (η,Dtot):
| (8) |
Inverting the relationships (6) to obtain
| (9) |
the parameters θop, η in Eq. (8) can be replaced by the performance measures, p(err) and 〈DT〉, yielding a unique, parameter-free relationship describing the speed-accuracy tradeoff that maximizes RR:
| (10) |
Eq. (10) defines an optimal performance curve (OPC) [4], shown in Fig. 1(a) Each point (p(err), 〈DT〉/Dtot) along the OPC corresponds to an optimal threshold-to-drift ratio θop specified by Eq. (8) which, in turn, is associated with a particular decision time and error rate combination that maximize RR: any other threshold, lower or higher, associated with responses that are faster or slower (diamonds in Fig. 1(a)), yields smaller net rewards. Different points on the curve represent θop’s and corresponding speed-accuracy trade-offs for different values of η (i.e., task difficulty) and Dtot (i.e., task timing). Critically, the shape of the OPC itself is parameter free. Thus, it can be used to assess performance with respect to optimality and compare this across conditions, tasks, and even individuals, irrespective of differences in task difficulty or timing.
The OPC’s shape may be intuitively understood by observing that very noisy stimuli (η ≈ 0) contain little information, so that, if they are equally likely, it is optimal to choose at random, giving p(err) = 0.5 and 〈DT〉 = 0 (cf. SNR = 0.1 at the right of Fig. 1(a)). At its left, as η → ∞, stimuli become so easy to discriminate that both 〈DT〉 and p(err) approach zero (cf. SNR = 100). For intermediate SNRs it is advantageous to accumulate evidence for just long enough (e.g., SNRs = 1 and 10). Thus, to maximize rewards, optimal performance is achieved by balancing speed versus accuracy, and not by systematically favoring accuracy. Human data appear to present a challenge to this model, as we now consider.
2.3 Experimental evidence: Failures to optimize
Two 2AFC experiments [4, 5] have directly tested whether humans optimize reward rate in accord with the OPC derived above. In the first, 20 participants viewed motion stimuli [9] and were rewarded for each correct discrimination. The experiment was divided into 7-minute blocks with different response to stimulus intervals in each block. In the second, 60 participants discriminated if the majority of 100 locations on a static display were filled with stars or empty. Blocks lasted for 4 minutes, and two difficulty conditions were used. In all cases participants were instructed to maximize their total earnings, and unrewarded practice blocks were administered before testing began.
As noted above, one of the appeals of the OPC is that it is independent of the parameters defining the DD process, with Dtot entering only as the denominator in Eq. (10). This allows data to be pooled across all participants and task conditions. That is, findings concerning actual performance can be compared with optimal performance irrespective of task difficulty, timing or individual differences. For the experiments of [4, 5], 〈DT〉’s were estimated by fitting the DD model to reaction time distributions, the 0 − 50% error rate range was divided into 10 bins, and 〈DT/Dtot〉 were computed for each bin by averaging over those results and conditions with error rates in that bin. This yields the open (tallest) bars in Fig. 1(b); the shaded bars derive from similar analyses restricted to subgroups of participants ranked by their total rewards accrued over all blocks of trials and conditions.
The top 30% group clearly performs close to the OPC, supporting the DD model as an account of human decision making performance, and the conjecture that (at least some) participants can achieve near-optimal performance. Nonetheless, a majority achieve substantially lower total scores. Interestingly, this is due to longer decision times and greater accuracy than are required to maximize reward rate [5]. This particular pattern of deviations from optimality raises two possibilities: 1) Participants seek to optimize some other criterion of performance, such as accuracy, in place of, or in addition to, maximizing monetary reward. 2) Participants seek to maximize reward, but fall short in a systematic way due to specific constraint(s) on performance and/or the influence of other cognitive factor(s). We address these possibilities in the following sections.
2.4 A preference for accuracy?
There is a longstanding literature that suggests humans favor accuracy over speed in reaction time tasks (e.g., [52]). This could explain the observations in Fig. 1(b), insofar as decision times that are longer than optimal are typically associated with more accurate responses. Participants may try to maximize accuracy in addition to (or even instead of) rewards, as postulated in [46, 6]. This can be formalized by combining accuracy with reward rate in at least two ways [4]:
| (11) |
The first (RA) subtracts a fraction of error rate from RR of Eq. (7); the second (RRm) penalizes errors by reducing previous winnings. Critically, both include a free parameter q ∈ (0, 1) that specifies the relative weight placed on accuracy. Increasing q drives the OPC upward [4, Fig. 13], consistent with the empirical observations shown in Fig. 1(b), suggesting that participants may indeed include accuracy in their objective function. One reason for this may be that they (incorrectly) assume that errors are explicitly penalized, at least early during their experience with the task. This possibility is addressed by further empirical findings discussed below.
However, there are at least two alternative accounts of the data that preserve the assumption that participants seek primarily to optimize rewards. One is that timing uncertainty corrupts estimates of reward rate, systematically biasing performance toward longer decision times. The other is that participants factor into their estimates of reward rate the costs associated with fine-grained adjustment of parameters (such as response threshold), the advantages of which may be small relative to those costs. We consider each of these in turn, and compare them with accuracy-based models in their abilities to account for empirical data.
2.5 Robust decisions in the face of uncertainty?
In the analyses of §2.2 and §2.4 it is assumed that participants maximize an objective function for the DD model, given the exact task parameters. However, it is unlikely that participants can perfectly infer these. For example, RR depends on inter-trial delays as well as SNR. Delays, in particular, may be hard to estimate. Information-gap theory [3] allows parameters to lie within a bounded uncertainty set, and uses a maximin strategy to identify parameters that optimize a worst case scenario.
Interval timing studies [12] indicate that time estimates are normally distributed around the true duration with a standard deviation proportional to it [26]. This prompted the assumption in [85] that the estimated delay Dtot lies in a set Up(αp; D̃tot) = {Dtot > 0 : |Dtot − D̃tot| ≤ αp D̃tot}, of size proportional to the actual delay D̃tot, with presumed level of uncertainty αp analogous to the coefficient of variation in scalar expectancy theory [26]. In place of the optimal threshold of Eq. (8), the maximin strategy selects the threshold θMM that maximizes the worst RR that can occur for Dtot ∈ Up(αp; D̃tot). For uncertainties in delay, it predicts a one-parameter family of maximin performance curves (MMPCs) that are scaled versions of the OPC (10):
| (12) |
where γ ≡ D̃tot/Dtot [85]. Like the objective functions (11) that emphasize accuracy, these curves also predict longer mean decision times than the OPC (10). Uncertain SNRs can be treated similarly, yielding families of MMPCs that differ from both the OPC Eq. (10) and MMPC for timing uncertainty Eq. (12), rising to peaks at progressively smaller p(err) as uncertainty increases. An alternative strategy, also investigated in [85], yields robust-satisficing performance curves (RSPCs) that provide poorer fits and thus are not discussed here.
Fig. 2 shows data fits to the parameter-free OPC, the objective functions of Eq. (11), to MMPCs for timing uncertainty and SNR, and to RSPCs for timing uncertainty. While there is little difference among fits to the top 30%, data from the middle 60% and lowest 10% subgroups exhibit patterns that distinguish among the theories. Maximum likelihood computations show that MMPCs for uncertainties in delays provide the best fits, followed by RSPCs for uncertainties in delays and RA [85]. These findings indicate that optimizing reward rate given timing uncertainty leads to slower and more accurate decisions than those predicted by the OPC, which assumes perfect knowledge of delays. Greater accuracy can be considered a consequence of maximizing reward rate under uncertainty, and not the objective of optimization.
2.6 Experimental evidence: Practice and timing uncertainty
To test whether deviations from the OPC can be better explained by an emphasis on accuracy or by timing uncertainty, Balci et al. [2] conducted a 2AFC experiment with motion stimuli encompassing a range of discriminabilities (moving dot displays with 0%, 4%, 8%, 16% and 32% coherences [9], kept fixed in each block), and administered interval timing tests in parallel [12]. 17 participants completed at least 13 sessions in each condition, insuring the greatest likelihood of achieving optimal performance by providing participants with extensive training, and affording the opportunity to examine practice effects [19, 53]. Four main results emerged, three of which we now summarize; the fourth is described in §3.2.
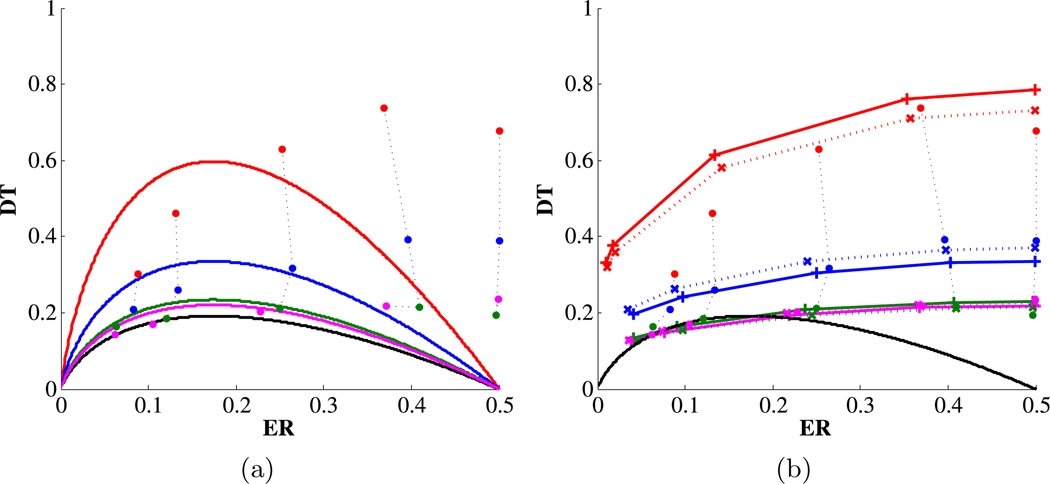
First, average performance converges toward the OPC with increasing practice. Fig. 3(a) shows the mean normalized decision times (dots) for five error bins averaged over sessions 1, 2–5, 6–9 and 10–13. Performance during the final two sets of sessions is indistinguishable from the OPC for higher coherences, but decision times remain significantly above the OPC for the two lowest coherences.
Figure 3.
Mean normalized decision times (dots) grouped by coherence vs. error proportions for sessions 1 (red), 2–5 (blue), 6–9 (green) and 10–13 (pink). (a) Performance compared with the OPC (black) and with best-fitting MMPCs for each coherence condition. With training, performance converges toward the OPC, but DTs remain relatively high at high error rates. (b) Performance compared with DD fits to single threshold for all coherences. Solid and dotted horizontal lines connect model fits and dotted vertical lines connect data points from different sessions having the same coherence. Fits connected by solid lines exclude 0 and 4% coherences; fits connected by dotted lines include all five coherences; fits from sessions 6–9 and 10–13 almost superimpose. Fits to a single threshold better capture longer DTs at high error rates relative to OPC and MMPCs. Panel (b) adapted from [2].
Second, the accuracy-weighted objective function RRm of Eq. (11) is superior to the OPC in fitting decision times across the full range of error rates during the early sessions, with accuracy weight decreasing monotonically through sessions 1−9 and thereafter remaining at q ≈ 0.2 (not shown here, see [2, Fig. 9]), suggesting that participants may indeed favor accuracy early during training, but that this diminishes with practice. This is consistent with the idea that participants come to such tasks expecting that errors are associated with explicitly negative outcomes (e.g., immediate losses, as may be common in real world settings), rather than being limited to opportunity costs (as assumed by the OPC). With practice, they may adjust their beliefs to accord with the fact that errors incur only opportunity costs.
Third, as shown in Fig 4, deviations from the OPC are stably related to timing ability. Throughout training, the timing inaccuracy of participants, independently assessed by their coefficients of variation in a peak-interval timing task [56], is significantly positively correlated with their distance from the OPC [2]. Furthermore, this relationship provides a better account of deviations from the OPC than emphasis on accuracy (as indexed by the weight parameter q in the objective function RRm). This suggests that participants may choose decision parameters that maximize reward rate, taking into account their timing uncertainty as discussed in the previous section.
Figure 4.
Mean square deviation of decision times from OPC vs. interval timing coefficients of variation for individual participants, averaged over all coherences and sessions 2–13. Line shows linear regression fit.
Collectively, these results support the hypothesis that, given sufficient practice, humans can learn to approach optimal performance (maximizing rewards) by devaluing accuracy, with a deviation from optimality that is inversely related to timing ability. Nevertheless, MMPCs based on timing uncertainty fall short of fully capturing performance, especially for the two lowest coherences: Fig. 3(a). Thus, even after accounting for timing uncertainty, reward rates are suboptimal according to the DD model. This suggests that other factors may be involved.
One of these is persistent variability across trials. The extended DDM accounts for this by drawing drift rates A and starting points x(0) from distributions on each trial [60, 4], thus allowing slow and fast errors respectively. The former may explain deviations from the OPC seen for high error rates in Fig. 3(a). However, as yet there is no principled way to determine which factor (variability in drift vs. starting point) should dominate. Moreover, each additional parameter brings with it a family of OPCs (as in §§2.4–2.5), and analytical expressions are not available for those derived from extended DDMs. Both [2] and [70] (cf. §3.2 below) contain extended DDM fits in their optimality analyses, but we are unaware of any systematic studies of the effects of deviations from optimality due to such variability. In contrast, considering the costs of cognitive control may provide a normative account of these effects, to which we now turn.
3 The role of control in optimization
So far, our focus has been on optimization of performance in which task conditions are stationary: models have assumed fixed task parameters, and data were analyzed for the most part condition-by-condition (e.g., each coherence condition was considered independently in Fig. 3). However, in both the real world and the laboratory, task conditions change and participants must adapt their decision parameters accordingly. Cognitive control has been defined as the set of processes (and underlying mechanisms) responsible for assessing task conditions and outcomes and adjusting behavior accordingly [50]. We now review work that begins to explore the role of control processes in optimization, and their influence on the dynamics of performance.
3.1 The cost of control
It has long been recognized that cognitive control is associated with mental effort [54]. Accordingly, the effort associated with adjusting parameters as conditions change (i.e., engagement of control) may register as a cost. The fourth finding of Balci et al. [2] supports the hypothesis that participants may take account of such costs, and weigh them against benefits that would accrue from optimizing performance for each task condition. The OPCs of Fig 3 assume that the decision threshold was optimized for the coherence (SNR) in each block. However, block-by-block adjustments would engage cognitive control that may have been perceived as effortful. Accordingly, especially if the benefits of such adjustments were small, participants may have sought a single threshold that does best over all conditions, relieving them of the need to estimate coherences and adjust thresholds from block to block.
To assess this possibility, Balci et al. [2] computed the single threshold that was optimal when applied over all coherence conditions. Fig. 3(b) shows that the resulting curve fits the full range of performance for the later sessions (6–13), suggesting that, at least with practice, participants came to adopt a single threshold that maximized reward across all conditions. Consistent with this strategy, it was found that rewards for this single threshold differed minimally from those accrued using the individual thresholds, optimized for the different conditions. Thus, the cost-benefit tradeoff appears to have weighed against exercising control on a condition-by-condition basis, and in favor of a single threshold. Hence, allowing for presumed costs of control, participants may have indeed been optimizing performance.
The analysis above highlights the need for an independent assessment of the costs of control. Recent work has begun to quantify costs associated with cognitive control [8], and to incorporate these in formal analyses of behavioral performance (e.g., [73]). Insofar as such costs offset the rewards associated with performance, a better understanding of these, and factoring them into analyses of behavior, promises to permit more accurate assessments of the extent to which people perform optimally. That said, there is increasing evidence that, under many circumstances, people do actively adjust decision parameters in response to changes in task conditions [55, 40, 45, 31, 42, 34]. Information needed to make such adjustments can come from several sources, including prior experience (i.e., expectations), the current stimulus, and assessments of the outcome of performance itself (e.g., accuracy, speed, processing conflict, confidence, etc.).
Recent studies have begun to address the mechanisms responsible for making such adjustments, with a particular focus on how they are driven by performance outcomes [7, 35, 81, 11, 69, 39]. However, few of these studies have involved normative models that explicitly address the extent to which adjustments in decision parameters serve optimization. Below, we review two areas of recent work that attempt to do this: one addresses trial-to-trial adjustments based on prior knowledge, and the other considers the dynamics of adjustment within individual trials under stimulus variability.
3.2 Prior expectations and trial-to-trial adjustments
Given prior information on the probability of observing each stimulus in a 2AFC task, a DD process can be optimized by appropriately shifting the initial condition; biased rewards favoring one response over the other can be accommodated in a similar manner [4]. Comparisons of these predictions with human behavioral data were carried out in [70]. As in the experiments described above, stimulus discriminability and other conditions were fixed over each block of trials. On average participants achieved 97 − 99% of maximum reward, and some performed essentially optimally.
A related study of monkeys used a cued-response paradigm with a fixed stimulus presentation period that relieves the need for a speed-accuracy tradeoff, but in which motion coherences varied randomly from trial to trial, and differences in reward contingencies for the two responses were signaled before each trial. The monkeys came within 0.5% and 2% respectively of maximum possible rewards by adjusting the balance between preferring the higher reward and accurately assessing the noisy stimulus [24]. This implies appropriate shifts in the psychometric (accuracy vs. discriminability) function depending on coherence, which can be effected by either biasing drift rates, or by shifting initial conditions. That the latter is more likely was established in [62] by fitting LIP recordings. Behavioral studies of humans discriminating low aspect ratio rectangles also revealed near-optimal shifts in initial conditions in response to changes in reward bias [25].
In the above cases, participants were shown to perform (near) optimally based on their estimates of stimulus or reward probabilities, when explicitly informed of them. Humans also exhibit adjustment effects in response to patterns of repetitions and alternations that necessarily occur in random sequences, presumably based on a general expectation that locally observed patterns will persist or recur. Models that address RT and accuracy effects reflective of such adjustments appear in [14, 38, 37, 30]. These models further support the view that participants adapt by shifting the initial conditions of the decision process. While such adjustments typically degrade performance in response to truly random sequences (they are suboptimal), the ability to extract patterns in natural situations is advantageous, since it allows people to adapt prior beliefs to better match context-specific, stationary (or slowly changing) environments, once they have learned relevant statistics. This possibility is explored in [83].
3.3 Stimulus variability and within-trial adjustments
The work described in the previous subsection indicates that participants make trial-to-trial adjustments in decision parameters, especially when patterns are present or apparent in the sequence of stimuli. Modeling work has also suggested that participants can adapt decision parameters within trials, especially when task conditions vary from trial to trial. For example, in 2AFC experiments with mixed motion coherences it has been proposed that slow decisions, typically associated with low SNR and lack of confidence, may be accelerated by a monotonically-rising “urgency” signal corresponding to increasing drift rate, a proposal supported by fits to LIP recordings [33]. A recent analysis of DD models applied to variable discriminability stimuli shows that drift rate adjustments are suboptimal compared to setting initial conditions [76], but also that human participants appear to combine the two strategies in a similar manner for both fixed and variable discriminability, in contrast to the claims that drift rate bias should dominate in the latter case [33], and that this is necessary for optimality [80].
The Eriksen flanker task [23] has also been used to study within-trial dynamics of processing and attentional control (e.g., [31, 18, 7]). In this task participants carry out a standard 2AFC on a central stimulus, flanked by stimuli that either invite the same response (compatible) or its alternative (incompatible). Accuracy is lower for incompatible trials and, plotted against RT, displays a dip below 50% followed by a rise to the same asymptote as for compatible trials: see [31, Fig. 1]. The network model of [18] suggested that these effects could be explained by dynamic shifts of attention within each trial. In this model separate units accumulate bottom-up perceptual evidence from the central and flanker stimuli while subject to top-down attentional influences [18, Fig. 8], so that processing of the central stimulus eventually prevails. Subsequently, [43] showed that shifting attention can be captured by a time varying drift rate A(t) in a one-dimensional OU model. Representing A(t) as a sum of exponentials, it was possible to fit accuracy/RT data and RT distributions with fewer parameters than the network of [18].
A normative interpretation has been provided by a Bayesian analysis that models task performance as dynamic updating of the joint probability distribution for stimulus identity and trial type (compatible/incompatible) [82]. Updating Bayesian posteriors may seem unrelated to the model of [18] or its reduction [43], but for Gaussian stimulus probabilities with sufficiently large variance, it can be well-approximated by a set of uncoupled DD processes that allow analytical estimation of the evolving posteriors, and hence of accuracy and RT distributions [44]. These also fit the data of [18], suggesting both that participants adjust decision parameters within each trial, and that the network of [18] represents a neurally-plausible model of this (near-) optimal computation.
3.4 Exploration, exploitation, and neuromodulation
Thus far, we have focused on studies that examine performance in the context of a particular task. While the decision parameters optimal for that task may vary over stimuli, more general task features have remained constant (e.g., the domain of the stimuli, responses and rewards, the relevant set of stimulus-response mappings, etc.). Under such stationary conditions, good performance implies exploitation of a well-defined strategy. However, real world conditions can change, requiring exploration of different possible goals (i.e., what new tasks should be performed). This typically involves foregoing immediate rewards in the service of greater ones over the longer term. Balancing this tradeoff involves a higher level form of optimization. While there is no general solution to this problem, a growing body of research seeks to understand how organisms, including humans, manage the exploitation/exploration tradeoff [17].
One theory proposes that the neuromodulatory brainstem nucleus locus coeruleus (LC) contributes to regulating this balance, by dynamically modulating neural responsivity through the phasic release of norepinephrine (NE) [66, 74, 1]. According to this Adaptive Gain Theory, transient increases in LC-NE activity promote exploitation by increasing the gain of task-relevant processes, and thereby optimize performance of the current task [10, 68]. In contrast, sustained (and therefore task-indiscriminate) increases in LC-NE activity favor off-task processes, promoting exploration. Shifts between these modes are driven by ongoing assessments of task utility, such that sustained increases favor exploitation, while prolonged decreases favor exploration [1]. A closely-related proposal suggests that fluctuations in uncertainty can similarly drive the LC-NE system [84].
These mechanisms were implemented in a reinforcement learning (RL) model of reversal learning [48]. This study showed that including the LC-NE gain regulation mechanism and a simple cortical performance monitoring mechanism in a standard RL model dramatically improved the system’s ability to adapt to changes in reinforcement contingencies, and provided a qualitative fit to both behavioral data and direct recordings from the LC in monkeys performing a reversal task [16]. Following reversals, the combined effects of gain modulation and RL allowed fast transitions from exploration to exploitation, whereas with RL alone such transitions were associated with substantially higher ERs that persisted for longer. Subsequent studies in humans have used the observation that pupil diameter closely tracks LC activity [1] to demonstrate that engagement of the LC-NE system conforms to predictions about its role in regulating the explore/exploit tradeoff [22, 27, 36, 51]. Further work remains to more rigorously test the extent to which this is achieved optimally, under suitably constrained conditions.
3.5 Physiological constraints?
Most of the theoretical work reviewed above is based on relatively abstract models. While these have provided important insights into constraints on optimality at the systems level, they do not address constraints that may arise from the underlying neural circuits. Explorations of these have begun by relating abstract models to biophysical aspects of neural function. For example, spiking-neuron models can be reduced in dimension by averaging over populations of cells [79, 21], allowing them to include the effects of synaptic time constants and neurotransmitters such as NE [20].
The resulting nonlinear differential equations are more complex than the LCA Eqs. (1–2), and unlike the optimal DD process of Eq. (5), they can possess multiple stable states [79, Figs. 4–5], [21, Fig. 13]. Even when there is an attracting curve, nonlinear dynamics can cause suboptimal integration, and deviations from the curve can blur the decision thresholds [77, Fig. 7]. Adjustments in baseline activity and gain can keep accumulators in near-linear dynamical ranges [66, 15], but the nonlinear effects suggest that there are physiological obstructions to optimality, especially when task conditions span a wide range. Improvements of low-dimensional models, derived from biophysically-detailed neural networks and coupled with multi- unit and multi-area recordings, may help determine whether and how such constraints cause significant deviations from optimality.
4 Summary and conclusions
We have reviewed leaky accumulator and drift-diffusion models of 2AFC decision making and shown how the latter can generate normative descriptions of optimal performance (§§2.1–2.2). These low-dimensional models are fast to simulate, describe behavior remarkably well [75, 28, 29, 71], admit analytical study [10, 4], and provide understanding of mechanisms. They have generated experiments that revealed failures to optimize (§2.3), and motivated the prediction that optimality demands accurate timing ability (§2.5) as well as accounting for the costs of control. Further experiments revealed that, while practice can improve participants’ strategies, their asymptotic performance is indeed correlated with timing ability (§2.6), and that data across a wide range of stimulus discriminability were also consistent with a single, fixed decision threshold that minimized the costs of control. The explicit OPC expression (10), derived from the simple DD model, was crucial to this procedure; we doubt that such predictions could as readily emerge from computational simulations alone. Furthermore, the parameter-free OPC provides a normative benchmark against which choices of speed-accuracy tradeoffs can be assessed and compared across different tasks, conditions and individuals, irrespective of task difficulty and/or timing.
More fundamentally, tests of optimality require precise definitions of objective functions and clear understanding of how decision making processes are parameterized to achieve them, raising questions about cognitive control, including its costs (§3.1) and roles in modulating behavior in changing environments (§§3.2–3.3). The tradeoff between exploitation and exploration is also attracting much attention, as described in §3.4. Such studies of more complex behaviors than binary decisions will suggest more sophisticated objective functions, and thus enable more realistic optimality assays.
The call for this special issue noted that bounds to optimal performance may be set explicitly, imposed by the task environment, by experience, or by the information-processing architecture. The statistically-stationary 2AFC task, implicitly requiring maximization of reward rate, exemplifies both explicit setting, and imposition by environment (§§2.2–2.3). The modified reward rates, priors and sequential effects of §2.4 and §3.2 reflect human experience, and constraints due to timing ability (§§2.5–2.6). The costs of control and the nonlinear properties of spiking neurons (§3.5) exemplify constraints due to neural architecture. All these factors appear relevant in limiting performance. Nonetheless, they suggest that, given sufficient instruction and experience and allowing for intrinsic constraints, humans can approximate optimality, at least in simple 2AFC tasks.
Acknowledgments
This work was supported by AFOSR grants FA9550- 07-1-0537 and FA9550-07-1-0528 and NIH P50 MH62196. The authors thank Fuat Balci for providing Figs. 3–4, and gratefully acknowledge the contributions of many collaborators, not all of whose work could be described in this article.
References
- 1.Aston-Jones G, Cohen JD. An integrative theory of locus coeruleus-norepinephrine function: Adaptive gain and optimal performance. Annu. Rev. Neurosci. 2005;28:403–450. doi: 10.1146/annurev.neuro.28.061604.135709. [DOI] [PubMed] [Google Scholar]
- 2.Balci F, Simen P, Niyogi R, Saxe A, Holmes P, Cohen JD. Acquisition of decision making criteria: Reward rate ultimately beats accuracy. Attention, Perception & Psychophysics. 2011;73(2):640–657. doi: 10.3758/s13414-010-0049-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ben-Haim Y. Information Gap Decision Theory: Decisions under Se- vere Uncertainty. 2nd Edition. New York: Academic Press; 2006. [Google Scholar]
- 4.Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: A formal analysis of models of performance in two alternative forced choice tasks. Psychol. Rev. 2006;113(4):700–765. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- 5.Bogacz R, Hu P, Cohen JD, Holmes P. Do humans produce the speed-accuracy tradeoff that maximizes reward rate? Quart. J. Exp. Psychol. 2010;63:863–891. doi: 10.1080/17470210903091643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bohil CJ, Maddox WT. On the generality of optimal versus objective classifier feedback effects on decision criterion learning in perceptual categorization. Memory & Cognition. 2003;31(2):181–198. doi: 10.3758/bf03194378. [DOI] [PubMed] [Google Scholar]
- 7.Botvinick M, Braver T, Barch D, Carter C, Cohen JD. Conflict monitoring and cognitive control. Psychol. Rev. 2001;108(3):625–652. doi: 10.1037/0033-295x.108.3.624. [DOI] [PubMed] [Google Scholar]
- 8.Botvinick MM, Huffstetler S, McGuire J. Effort discounting in human nucleus accumbens. Cognitive, Affective and Behavioral Neu- rosci. 2009;9:16–27. doi: 10.3758/CABN.9.1.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Britten KH, Shadlen MN, Newsome WT, Movshon JA. Responses of neurons in macaque MT to stochastic motion signals. Visual Neurosci. 1993;10:1157–1169. doi: 10.1017/s0952523800010269. [DOI] [PubMed] [Google Scholar]
- 10.Brown E, Gao J, Holmes P, Bogacz R, Gilzenrat M, Cohen JD. Simple networks that optimize decisions. Int. J. Bifurcation and Chaos. 2005;15(3):803–826. [Google Scholar]
- 11.Brown JW, Braver TS. Learned predictions of error likelihood in the anterior cingulate cortex. Science. 2005;307(5712):1118–1121. doi: 10.1126/science.1105783. [DOI] [PubMed] [Google Scholar]
- 12.Buhusi CV, Meck WH. What makes us tick? functional and neural mechanisms of interval timing. Nature. 2005;6:755–765. doi: 10.1038/nrn1764. [DOI] [PubMed] [Google Scholar]
- 13.Busemeyer JR, Townsend JT. Decision field theory: A dynamiccognitive approach to decision making in an uncertain environment. Psychological Review. 1993;100:432–459. doi: 10.1037/0033-295x.100.3.432. [DOI] [PubMed] [Google Scholar]
- 14.Cho RY, Nystrom LE, Brown ET, Jones AD, Braver TS, Holmes P, Cohen JD. Mechanisms underlying dependencies of performance on stimulus history in a two-alternative forced-choice task. Cog. Affect, & Behav. Neurosci. 2002;2(4):283–299. doi: 10.3758/cabn.2.4.283. [DOI] [PubMed] [Google Scholar]
- 15.Cohen JD, Dunbar K, McClelland JL. On the control of automatic processes: A parallel distributed processing model of the Stroop effect. Psychological Review. 1990;97(3):332–361. doi: 10.1037/0033-295x.97.3.332. [DOI] [PubMed] [Google Scholar]
- 16.Cohen JD, McClure SM, Gilzenrat M, Aston-Jones G. Dopamine-norepinephrine interactions: Exploitation vs. exploration. Neuropsychopharmacology. 2005;30:S1–S28. [Google Scholar]
- 17.Cohen JD, McClure SM, Yu AJ. Should I stay or should I go? How the human brain manages the tradeoff between exploitation and exploration. Phil. Trans. Roy. Soc. B, Lond. 2007;362(1481):933–942. doi: 10.1098/rstb.2007.2098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cohen JD, Servan-Schreiber D, McClelland JL. A parallel distributed processing approach to automaticity. Amer. J. of Psychol. 1992;105:239–269. [PubMed] [Google Scholar]
- 19.Dutilh G, Vandekerckhove J, Tuerlinckx F, Wagenmakers EJ. A diffusion model decomposition of the practice effect. Psychonom. Bull. Rev. 2009;16(6):1026–1036. doi: 10.3758/16.6.1026. [DOI] [PubMed] [Google Scholar]
- 20.Eckhoff P, Wong KF, Holmes P. Optimality and robustness of a biophysical decision-making model under norepinephrine modulation. J. Neurosci. 2009;29(13):4301–4311. doi: 10.1523/JNEUROSCI.5024-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Eckhoff P, Wong K-F, Holmes P. Dimension reduction and dynamics of a spiking neuron model for decision making under neuromodulation. SIAM J. on Applied Dynamical Systems. 2011;10(1):148–188. doi: 10.1137/090770096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Einhäuser W, Stout J, Koch C, Carter OL. Pupil dilation reflects perceptual selection and predicts subsequent stability in perceptual rivalry. Proc. Nat. Acad. Sci. U.S.A. 2008;105:1704–1709. doi: 10.1073/pnas.0707727105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Eriksen BA, Eriksen CW. Effects of noise letters upon the identification of target letters in a non-search task. Perception and Psychophysics. 1974;16:143–149. [Google Scholar]
- 24.Feng S, Holmes P, Rorie A, Newsome WT. Can monkeys choose optimally when faced with noisy stimuli and unequal rewards? PLoS Comput. Biol. 2009;5(2):e1000284. doi: 10.1371/journal.pcbi.1000284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gao J, Tortell R, McClelland JL. Dynamic integration of reward and stimulus information in perceptual decision-making. PLoS ONE. 2011;6(3):e16749. doi: 10.1371/journal.pone.0016749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gibbon J. Scalar expectancy theory and Weber’s law in animal timing. Psychol. Rev. 1977;84(3):279–325. [Google Scholar]
- 27.Gilzenrat MS, Nieuwenhuis S, Cohen JD. Pupil diameter tracks changes in control state predicted by the adaptive gain theory of locus coeruleus function. Cognitive, Affective and Behavioral Neurosci. 2010;10:252–269. doi: 10.3758/CABN.10.2.252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gold JI, Shadlen MN. Neural computations that underlie decisions about sensory stimuli. Trends in Cog. Sci. 2001;5(1):10–16. doi: 10.1016/s1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
- 29.Gold JI, Shadlen MN. Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron. 2002;36:299–308. doi: 10.1016/s0896-6273(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 30.Goldfarb S, Wong-Lin KF, Schwemmer M, Leonard NE, Holmes P. Can post-error dynamics explain sequential reaction time patterns? Frontiers in Psychology. 2012;3:213. doi: 10.3389/fpsyg.2012.00213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gratton G, Coles MG, Sirevaag EJ, Eriksen CW, Donchin E. Pre- and poststimulus activation of response channels: a psychophysiological analysis. J. Exp. Psychol.: Hum. Percept. Perform. 1988;14:331–344. doi: 10.1037//0096-1523.14.3.331. [DOI] [PubMed] [Google Scholar]
- 32.Grossberg S. Nonlinear neural networks: principles, mechanisms, and architectures. Neural Networks. 1988;1:17–61. [Google Scholar]
- 33.Hanks TD, Mazurek ME, Kiani R, Hopp E, Shadlen MN. Elapsed decision time affects the weighting of prior probability in a perceptual decision task. J. Neurosci. 2011;31(17):6339–6352. doi: 10.1523/JNEUROSCI.5613-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Henik A, Bibi U, Yanai M, Tzelgov J. The stroop effect is largest during first trials. Abstracts of the Psychonomic Society. 1997 [Google Scholar]
- 35.Holroyd CB, Coles MGH. The neural basis of human error processing: Reinforcement learning, dopamine, and the error-related negativity. Psychol. Rev. 2002;109(4):679–709. doi: 10.1037/0033-295X.109.4.679. [DOI] [PubMed] [Google Scholar]
- 36.Jepma M, Nieuwenhuis S. Pupil diameter predicts changes in the exploration-exploitation trade-off: Evidence for the adaptive gain theory. J. Cog. Neurosci. 2011;23:1587–1596. doi: 10.1162/jocn.2010.21548. [DOI] [PubMed] [Google Scholar]
- 37.Gao J, Wong-Lin KF, Holmes P, Simen P, Cohen JD. Sequential effects in two-choice reaction time tasks: Decomposition and synthesis of mechanisms. Neural Computation. 2009;21(9):2407–2436. doi: 10.1162/neco.2009.09-08-866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jones AD, Cho RY, Nystrom LE, Cohen JD, Brown ET, Braver TS. A computational model of anterior cingulate function in speeded response tasks: Effects of frequency, sequence, and conflict. Cog. Affect, & Behav. Neurosci. 2002;2(4):300–317. doi: 10.3758/cabn.2.4.300. [DOI] [PubMed] [Google Scholar]
- 39.Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science. 2009;324(5928):759–764. doi: 10.1126/science.1169405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Laming D. Choice reaction performance following an error. Acta Psychologica. 1968;43(3):199–224. [Google Scholar]
- 41.Laming DRJ. Information Theory of Choice-Reaction Times. New York: Academic Press; 1968. [Google Scholar]
- 42.Lindsay DS, Jacoby LL. Stroop process dissociations: The relationship between facilitation and interference. J. Exp. Psychol.: Hum. Percept. Perform. 1994;20:219–234. doi: 10.1037//0096-1523.20.2.219. [DOI] [PubMed] [Google Scholar]
- 43.Liu Y, Holmes P, Cohen JD. A neural network model of the Eriksen task: Reduction, analysis, and data fitting. Neural Computation. 2008;20(2):345–373. doi: 10.1162/neco.2007.08-06-313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Liu YS, Yu AJ, Holmes P. Dynamical analysis of Bayesian inference models for the Eriksen task. Neural Computation. 2009;21(6):1520–1553. doi: 10.1162/neco.2009.03-07-495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Logan GD, Zbrodoff NJ. When it helps to be misled: Facilitative effects of increasing the frequency of conflicting stimuli in a stroop-like task. Memory and Cognition. 7:166–174. 120. [Google Scholar]
- 46.Maddox WT, Bohil CJ. Base-rate and payoff effects in multidimensional perceptual categorization. J. Exp. Psychol. 1998;24(6):1459–1482. doi: 10.1037//0278-7393.24.6.1459. [DOI] [PubMed] [Google Scholar]
- 47.Mazurek ME, Roitman JD, Ditterich J, Shadlen MN. A role for neural integrators in perceptual decision making. Cerebral Cortex. 2003;13(11):891–898. doi: 10.1093/cercor/bhg097. [DOI] [PubMed] [Google Scholar]
- 48.McClure SM, Gilzenrat MS, Cohen JD. An exploration-exploitation model based on norepinephrine and dopamine activity. In: Weiss Y, Sholkopf B, Platt JC, editors. Advances in Neural Information Processing Systems. Vol. 18. Cambridge, MA: MIT Press; 2006. pp. 867–874. [Google Scholar]
- 49.Miller KD, Fumarola F. Mathematical equivalence of two common forms of firing rate models of neural networks. Neural Computation. 2012;24:25–31. doi: 10.1162/NECO_a_00221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Botvinick MM, Cohen JD. The computational and neural basis of cognitive control: Charted territory and new frontiers. 2012 doi: 10.1111/cogs.12126. (under review) [DOI] [PubMed] [Google Scholar]
- 51.Murphy PR, Robertson IH, Balsters JH, O’Connell RG. Pupillometry and P3 index the locus coeruleus noradrenergic arousal function in humans. Psychophysiology. 2011;48:1532–1543. doi: 10.1111/j.1469-8986.2011.01226.x. [DOI] [PubMed] [Google Scholar]
- 52.Myung IJ, Busemeyer JR. Criterion learning in a deferred decision making task. Amer. J. Psychol. 1989;102(1):1–16. [Google Scholar]
- 53.Petrov AA, Van Horn NM, Ratcliff R. Dissociable perceptuallearning mechanisms revealed by diffusion-model analysis. Psychonom. Bull. Rev. 2011;18(3):490–497. doi: 10.3758/s13423-011-0079-8. [DOI] [PubMed] [Google Scholar]
- 54.Posner MI, Snyder CRfR. Attention and cognitive control. In: Solso R, editor. Information Processing and Cognition: The Loyola Symposium. Hillsdale, N.J: Lawrence Erlbaum; 1975. [Google Scholar]
- 55.Rabbitt PMA. Errors and error-correction in choice-response tasks. J. Exp. Psychol. 1966;71:264–272. doi: 10.1037/h0022853. [DOI] [PubMed] [Google Scholar]
- 56.Rakitin BC, Hinton SC, Penney TB, Malapani C, Gibbon J, Meck WH. Scalar expectancy theory and peak interval timing in humans. J. Exp. Psychol.: Animal Behavior Processes. 1998;24:1–19. doi: 10.1037//0097-7403.24.1.15. [DOI] [PubMed] [Google Scholar]
- 57.Ratcliff R. A theory of memory retrieval. Psychol. Rev. 1978;85(1):59–108. [Google Scholar]
- 58.Ratcliff R, Cherian A, Segraves MA. A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of two choice decisions. J. Neurophysiol. 2003;90:1392–1407. doi: 10.1152/jn.01049.2002. [DOI] [PubMed] [Google Scholar]
- 59.Ratcliff R, Hasegawa YT, Hasegawa RP, Smith PL, Segraves MA. Dual-diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. J. Neurophysiol. 2006;97:1756–1774. doi: 10.1152/jn.00393.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ratcliff R, Van Zandt T, McKoon G. Connectionist and diffusion models of reaction time. Psychol. Rev. 1999;106(2):261–300. doi: 10.1037/0033-295x.106.2.261. [DOI] [PubMed] [Google Scholar]
- 61.Roitman J, Shadlen M. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci. 2002;22(21):9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rorie A, Gao J, McClelland JL, Newsome WT. Integration of sensory and reward information during perceptual decision-making in lateral intraparietal cortex (LIP) PLoS ONE. 2010;5(2):e9308. doi: 10.1371/journal.pone.0009308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Roxin A, Ledberg A. Neurobiological models of two-choice decision making can be reduced to a one-dimensional nonlinear diffusion equation. PLoS Comput. Biol. 2008;4(3):e1000046. doi: 10.1371/journal.pcbi.1000046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rumelhart DE, McClelland JL. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Cambridge, MA: MIT Press; 1986. [DOI] [PubMed] [Google Scholar]
- 65.Schall JD. Neural basis of deciding, choosing and acting. Nature Rev. Neurosci. 2001;2:33–42. doi: 10.1038/35049054. [DOI] [PubMed] [Google Scholar]
- 66.Servan-Schreiber D, Printz H, Cohen JD. A network model of catecholamine effects: Gain, signal-to-noise ratio, and behavior. Science. 1990;249:892–895. doi: 10.1126/science.2392679. [DOI] [PubMed] [Google Scholar]
- 67.Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- 68.Shea-Brown E, Gilzenrat M, Cohen JD. Optimization of decision making in multilayer networks: The role of locus coeruleus. Neural Computation. 2008;20:2863–2894. doi: 10.1162/neco.2008.03-07-487. [DOI] [PubMed] [Google Scholar]
- 69.Simen P, Cohen JD, Holmes P. Rapid decision threshold modulation by reward rate in a neural network. Neural Networks. 2006;19:1013–1026. doi: 10.1016/j.neunet.2006.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Simen P, Contreras D, Buck C, Hu P, Holmes P, Cohen JD. Reward rate optimization in two-alternative decision making: Empirical tests of theoretical predictions. J. Exp. Psychol.: Hum. Percept. Perform. 2009;35(6):1865–1897. doi: 10.1037/a0016926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends in Neurosci. 2004;27(3):161–168. doi: 10.1016/j.tins.2004.01.006. [DOI] [PubMed] [Google Scholar]
- 72.Stone M. Models for choice-reaction time. Psychometrika. 1960;25:251–260. [Google Scholar]
- 73.Todd MT, Botvinick MM, Schwemmer MA, Cohen JD, Dayan P. Normative analysis of task switching. Abstract No. 194.21. Society for Neuroscience Meeting. 2011 [Google Scholar]
- 74.Usher M, Cohen JD, Servan-Schreiber D, Rajkowsky J, Aston-Jones G. The role of locus coeruleus in the regulation of cognitive performance. Science. 1999;283:549–554. doi: 10.1126/science.283.5401.549. [DOI] [PubMed] [Google Scholar]
- 75.Usher M, McClelland JL. On the time course of perceptual choice: The leaky competing accumulator model. Psychol. Rev. 2001;108(3):550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- 76.van Ravenzwaaij D, Mulder MJ, Tuerlinckx F, Wagenmakers E-J. Do the dynamics of prior information depend on task context? An analysis of optimal performance and an empirical test. Frontiers in Cog. Neurosci. 2012;3:132. doi: 10.3389/fpsyg.2012.00132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.van Ravenzwaaij D, van der Maas HLJ, Wagenmakers EJ. Optimal decision making in neural inhibition models. Psychol. Rev. 2012;119(1):201–215. doi: 10.1037/a0026275. [DOI] [PubMed] [Google Scholar]
- 78.Wald A, Wolfowitz J. Optimum character of the sequential probability ratio test. Ann. Math. Statist. 1948;19:326–339. [Google Scholar]
- 79.Wong KF, Wang X-J. A recurrent network mechanism of time integration in perceptual decisions. J. Neurosci. 2006;26(4):1314–1328. doi: 10.1523/JNEUROSCI.3733-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Yang T, Hanks TD, Mazurek M, McKinley M, Palmer J, Shadlen MN. Incorporating prior probability into decision making in the face of uncertain reliability of evidence. Abstract No. 621.4. Society for Neuroscience Meeting. 2005 http://sfn.scholarone.com. [Google Scholar]
- 81.Yeung N, Botvinick MM, Cohen JD. The neural basis of error detection: Conflict monitoring and the error-related negativity. Psychol. Rev. 2004;111(4):931–959. doi: 10.1037/0033-295x.111.4.939. [DOI] [PubMed] [Google Scholar]
- 82.Yu A, Dayan P, Cohen JD. Dynamics of attentional selection under conflict: Toward a rational Bayesian account. J. Exp. Psychol.: Hum. Percept. Perform. 2009;35(3):700–717. doi: 10.1037/a0013553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Yu AJ, Cohen JD. Sequential effects: Superstition or rational behavior? In: Platt JC, Koller D, Singer Y, Roweis S, editors. Advances in Neural Information Processing Systems. Vol. 21. Cambridge, MA: MIT Press; 2009. pp. 1873–1880. [PMC free article] [PubMed] [Google Scholar]
- 84.Yu AJ, Dayan P. Uncertainty, neuromodulation, and attention. Neuron. 2005;46:681–692. doi: 10.1016/j.neuron.2005.04.026. [DOI] [PubMed] [Google Scholar]
- 85.Zacksenhouse M, Bogacz R, Holmes P. Robust versus optimal strategies for two-alternative forced choice tasks. J. Math. Psychol. 2010;54:230–246. doi: 10.1016/j.jmp.2009.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]