Abstract
Carcinoma cells frequently expand and invade from a confined lesion, or multicellular clusters, into and through the stroma on the path to metastasis, often with an efficiency dictated by the architecture and composition of the microenvironment. Specifically, in desmoplastic carcinomas such as those of the breast, aligned collagen tracks provide contact guidance cues for directed cancer cell invasion. Yet, the evolving dynamics of this process of invasion remains poorly understood, in part due to difficulties in continuously capturing both spatial and temporal heterogeneity and progression to invasion in experimental systems. Therefore, to study the local invasion process from cell dense clusters into aligned collagen architectures found in solid tumors, we developed a novel engineered 3D invasion platform that integrates an aligned collagen matrix with a cell dense tumor-like plug. Using multiphoton microscopy and quantitative analysis of cell motility, we track the invasion of cancer cells from cell-dense bulk clusters into the pre-aligned 3D matrix, and define the temporal evolution of the advancing invasion fronts over several days. This enables us to identify and probe cell dynamics in key regions of interest: behind, at, and beyond the edge of the invading lesion at distinct time points. Analysis of single cell migration identifies significant spatial heterogeneity in migration behavior between cells in the highly cell-dense region behind the leading edge of the invasion front and cells at and beyond the leading edge. Moreover, temporal variations in motility and directionality are also observed between cells within the cell-dense tumor-like plug and the leading invasive edge as its boundary extends into the anisotropic collagen over time. Furthermore, experimental results combined with mathematical modeling demonstrate that in addition to contact guidance, physical crowding of cells is a key regulating factor orchestrating variability in single cell migration during invasion into anisotropic ECM. Thus, our novel platform enables us to capture spatio-temporal dynamics of cell behavior behind, at, and beyond the invasive front and reveals heterogeneous, local interactions that lead to the emergence and maintenance of the advancing front.
Introduction
The ability of cancer cells to invade from a confined lesion into the surrounding stroma and adjoining tissues is a fundamental behavior that contributes significantly to progression of malignant disease and poor clinical outcomes. This invasion of cancer cells is often dictated by cues from the microenvironment that can be chemical, such as chemokine or cytokine gradients, or physical, such as matrix stiffness and organization1–3. Indeed, in many instances, the architecture of the surrounding stroma, particularly the extracellular matrix (ECM), plays a critical role in directing local invasion4, 5. For example, unique tumor-associated collagen signatures (TACS) are present in desmoplastic breast tumor stroma that influence local invasion and metastasis and correlate with poor prognosis in human patients6, 7. Among these are TACS-3, where collagen fibers are aligned and reorganized perpendicular to the tumor-stroma boundaries in and around the tumor mass to promote directed invasion of breast cancer cells by contact guidance6, 8. Similarly, guided invasion on white matter tracts in brain tumors can promote expansion and dispersion of the primary tumor mass, often with undesirable outcomes for the patient9, while recent studies reveal aligned collagen architectures in pancreatic ductal adenocarcinomas10, 11 that promote directed migration of pancreatic carcinoma cells11. Consistent with these findings, tracks of ECM have been identified independently as regulators of cell motility in vivo using a number of distinct model systems6, 12–15. Thus, it is becoming increasingly clear that aligned ECM architectures are not restricted to breast carcinomas and likely exist in many cancers to promote disease progression.
Since ECM architecture plays a fundamental role in disease progression, understanding the dynamics of the interactions between a mass of cancerous cells and the surrounding anisotropic ECM in 3D is vital in order to obtain a clear picture of malignant progression. Yet, to date, systems that enable the ability to image cell invasion dynamics in space and time from cell-dense clusters into defined tumor-relevant architectures have been limited. However, several in vitro assays have been reported wherein a large cluster of cells interface and interact with an adjoining acellular collagen matrix either in the form of nested matrices6, 8, 16–19, or as organoids or explants, embedded with 3D collagen gels8, 20. In most cases, these approaches do lead to collagen fiber reorganization and generation of contact guidance cues in the form of aligned collagen fibers due to cell contractile forces8, 16. However, matrix reorganization to generate tissue tracks and subsequent invasion in this environment are distinct processes, and thus the ability to decouple these processes is an essential basis for next-generation in vitro invasion assays.
In order to study 3D invasion of carcinoma cells into aligned stromal collagen and the fundamental cell dynamics at distinct locations along the invasion path, as well as disease progression behavior in time, we report a new method to interface a pre-aligned carcinoma-associated-fibroblast-reorganized collagen matrix with a carcinoma cell-dense tumor-like plug. We demonstrate that carcinoma cells interface with the adjacent aligned matrix in 3D and quantify cell dynamics in the developing and mature invasion fronts as cells advance into the cancer-mimetic stroma. We identify spatial and temporal heterogeneity in cell invasion dynamics and demonstrate that cells at distinct locations along the invasive front display differences in morphology and migration behavior, offering novel insight into the progression of carcinoma cell invasion into and through anisotropic ECM.
Results
Engineering 3D environments to image focal invasion in vitro
To develop a novel 3D invasion assay that captures tumor relevant ECM architecture, we first generated aligned collagen matrices using our previously reported method21. In this method, collagen matrices seeded with carcinoma-associated fibroblasts are constrained along one axis, inducing anisotropic contraction and collagen alignment along that axis (Fig.1a)21. Such collagen matrices have previously been shown to have a tensile elastic modulus on the order of 25 kPa22, which may be further enhanced by the anisotropic fiber distribution. Label-free visualization of the collagen structure within the decellularized construct was performed with second harmonic generation (SHG) microscopy (Fig. 1b) and subsequent analysis of the matrix was performed using the curvelet transform coupled to a fiber extraction algorithm23 (CT-FIRE) (Fig. 1b) to quantify the extent and quality of fiber alignment in each construct. To quantify alignment we developed an alignment index, defined as the spread of the angular distribution of fibers normalized to that of a uniform distribution, which allows us to robustly capture the degree of anisotropy in the matrix21. Using this metric, we observed that aligned matrices have alignment indices greater than 1.3, with high alignment observed at ≥1.5 and very highly aligned regions giving indices >2 (Fig.1b, c). The alignment indices of the constructs used here for the invasion assays were around 1.5 or greater.
Fig. 1. Novel 3D assay to mimic invasion into aligned stromal collagen.
(a) Decellularized collagen matrix pre-aligned by constrained contraction of carcinoma-associated fibroblasts as previously described1. Indicated dimensions represent the approximate length and width of the constructs before contraction, the thickness of the gels range from ~0.7-1mm (b) Representative SHG image of collagen fibers and analysis of matrix alignment using CT-FIRE and the (c) corresponding histogram demonstrating the anisotropic distribution of collagen fibers (quantification of the fiber distribution is shown with the Alignment Index). (d) Assay construction showing the setup before and after interfacing a pre-aligned matrix with a carcinoma cell-dense collagen or Matrigel plug. (e) XY and XZ planar views of fluorescently labeled carcinoma cells by multiphoton excitation (pseudo-colored red) with simultaneous SHG imaging of collagen fibers (pseudo-colored cyan) showing breast carcinoma cells from the seeded plug invading into the adjacent pre-aligned matrix (boundary demarcated by yellow dotted lines) after ~16hr. (f) Representative line intensities along the x and z axes from the images in (e) showing a prominent increase in collagen signal beyond the interface and co-localization of collagen and cell fluorescence signal at different depths indicating the location of the invasive front in 3D (Scale bars in e = 200 µm).
To develop a tumor invasion platform where cells invade into, and migrate through, aligned matrices that mimic aligned stromal collagen observed in carcinomas6, 11, we sought to generate a 3D interface between an ECM plug containing a high-concentration bolus of cancer cells with one end of the pre-aligned collagen matrix. We initially observed that seamlessly interfacing pre-formed aligned collagen matrices with a polymerizing ECM plug is challenging on several counts, which likely explains, in part, the lack of existing methods in the current literature to develop such interfaces for 3D cell invasion. First, the highly hydrophilic and water-retaining properties of collagen matrices make it extremely difficult to prevent “wicking” of the polymerizing plug onto the entire bulk surface of the pre-aligned matrix (Supplementary Fig.1a). Second, on a standard tissue culture dish, the polymerizing plug, even if localized to one end, tends to connect entirely on top of the pre-aligned matrix, thus creating a nearly 2D-like interface (Supplementary Fig.1b). We overcame these hurdles by introducing a few key modifications to the simple idea of pipetting a cell-seeded tumor-like plug suspension at one end of the pre-aligned matrix. We first partially air dried the pre-aligned matrix to decrease the amount of aqueous fluid at its surface, while retaining enough hydration to maintain its structural integrity (Supplementary Fig. 1b, c). Next while pipetting the cell-seeded collagen plug, the plate is tilted at an angle so that the surface tension-induced wicking is counteracted by gravity (Supplementary Fig. 1b, c). Lastly, we allow the plug and the end of the pre-aligned matrix to connect on a hydrophobic surface so that their mutual hydrophilicity spontaneously forces a 3D interface (Supplementary Fig. 1c).
To assemble the invasion assay, we first place a pre-aligned matrix on a tissue culture dish with a short overhang onto a parafilm-coated hydrophobic region, which is bounded on the other three sides by impermeable hydrophobic barriers (Fig.1d). Next, after having let the matrix partially air dry, we tilt the entire setup and pipette the cell-seeded collagen plug onto the hydrophobic region enclosed by the barriers and the pre-aligned matrix (Fig. 1d). The partially dried matrix, barriers, gravity, and the hydrophobic layer together confine the plug to the region where it is pipetted (Fig. 1d). In addition, the strong hydrophilic interaction between the plug and the overhang of the pre-made matrix on a hydrophobic surface forces the overhang to shift slightly upward into the polymerizing plug, thus allowing the latter to form a thin layer underneath the matrix, creating a 3D interface (Fig. 1d).
To image invasion dynamics we employ nonlinear imaging to simultaneously image cells and the collagen matrix. Using combined multiphoton excitation (MPE) of fluorescence signals in cells and SHG imaging of collagen, we visualized the initial stages of invasion from the plug into the aligned collagen (Fig. 1e, f). Three-dimensional image reconstruction of the interface clearly demonstrates MDA-MB-231 breast carcinoma cells within the 3D volume as they advanced into the aligned matrix (Fig. 1e, f), confirming the successful interface and assembly of the invasion assay. Furthermore, the simple and robust principles utilized in this protocol suggested to us that the approach could be extended to other hydrophilic ECMs and cell types. We evaluated the ability to interface with alternate ECMs by using the same methods to interface Matrigel plugs containing primary murine mammary carcinoma cells with the aligned collagen matrices. Consistent with our rationale, the ECMs composing Matrigel matrix effectively interfaced with the anisotropic collagen construct. Time-lapse imaging with combined MPE and SHG revealed that these primary cells invade as a collective, often forming strands of advancing cells into the aligned matrix, in contrast to the single cell dissemination of MDA-MB-231 cells (Supplementary Movie 1, Fig. 1e, f), suggesting that the invasion platform presented here may be sufficient to capture and parse out distinct invasion behaviors and multiple invasion and migration modes, which are known to be present during cancer progression3.
Spatio-temporal evolution of invasion into aligned collagen
To capture and quantify invasion over time, we focused on quantifying cell dynamics using the highly invasive triple-negative MDA-MB-231 cell line. After the interface is generated between the cell-dense plug and the aligned ECM, MDA-MB-231 cells begin to spontaneously invade into the aligned matrix through an invasive front that develops, matures, and advances over time (Fig. 2a). This in effect advances the boundary of the tumor-like plug into the stromal collagen over time, much like a malignant lesion would expand into the surrounding tissue. Indeed, we can monitor these changes by imaging the engineered construct periodically using simultaneous MPE and SHG to visualize both cells and collagen, respectively (Fig. 2a, Supplementary Fig. 2a, c, e). To quantify the percentage of cells embedded within the matrix versus on top of it, we calculated the matrix and cell layer thicknesses and the fractional overlap between them at various time points using the three-dimensional image reconstructions. (Supplementary Fig. 2b, d, f). On an average, ~75–80% of the cell fluorescence signal overlaps with the SHG signal, indicating that the majority of the invasion front advances through the aligned matrix, although some cells migrate on top of the aligned matrix (Supplementary Fig. 2a-f). Furthermore, there were some notable variations of the collagen layer thickness and the percent overlap along the length of the gel. Behind the interface, the fraction overlap was lower with the thickness of the cell layer being larger than that of the collagen layer in the region where the highly cell dense plug interfaces with the pre-aligned matrix (Supplementary Fig. 2b,d,f). The thickness of the layers as well as the overlap tend to assume lower values close to the interface for earlier time points, owing to the local contraction resulting from the attachment of the plug and the partial drying of the pre-aligned matrix overhang on the hydrophobic layer (Supplementary Fig. 2b,d,f). Note that this effect is not as pronounced in all cases, as the example interface shown in Fig. 1e demonstrates a much smoother interface with more consistent cell, matrix layer thickness and overlap near the interface. Nevertheless, we primarily focused our analyses further along the invasion front, where the overlap is high, ranging between 0.8 and 1 and the collagen layer thickness remains largely constant, with SHG imaging measured thickness around 150–200µm (Supplementary Fig. 2b,d,f). This is considerably lower than the native pre-aligned matrices (700–1000µm) before integration into this assay, largely due to the partial drying of the matrix during assembly, which therefore suggests the matrix is it at least 4–5 times more dense than its original state. Overall, these results indicate the formation and maintenance of a 3D invasion interface over time. Although some cells near the interface are forced to the surface of the matrix due to the very high cell density, the large majority of cells remain embedded and invade through the matrix, thus enabling tracking and analysis of 3D invasion over time.
Fig. 2. Analysis of the invasive front during carcinoma cell invasion into 3D aligned collagen.
(a) Fluorescence micrographs showing typical, progressively advancing fronts of MDA-MB-231 cells into the aligned collagen matrix over 7 days, with the left edge of each image coincident with the approximate location of the interface. (b) Associated average intensity profiles over distance demonstrating the characteristic shape of the advancing fronts; dotted lines represent smoothed intensity profiles while solid lines show the Gaussian fits of the corresponding intensity profiles centered at the interface.
Examining invasion over 7 days, we observed that cells at the leading edge of the invasive front can advance greater than a millimeter from the interface, with many cells traveling several millimeters into the collagen matrix (Fig. 2a). To quantify invasion over time we utilized the average cell fluorescence intensity along the direction of invasion from maximum intensity projection images as a measure of the number of cells at each position along the front (Fig. 2b). Interestingly, the distribution of invading cells conform quite well to a Gaussian distribution centered at the interface between the cell-dense plug and the aligned matrix at early time points, but tend to shift to a more sigmoidal nature at later time points (Fig. 2b). This shift arises mainly due to the emergence of a new region of spatially unvarying high cell density close to the initial interface as the front invades further into the matrix. In the developing front at early time points, this region of high density exists within the plug (i.e., behind the tumor boundary/interface) and hence is excluded from the analysis. Thus, when taken in its entirety, the cell density profile from the bulk of the cell dense tumor-like plug to the edge remains similar in shape in both early and late stages as the entire front advances into the stroma over time (Fig. 1f, Fig. 2b). Consequently, at any given time point, the half width at half maximum of the fitted Gaussian can be employed as a representative metric of the distance of the invasion front from the tumor-stromal interface. Using this metric, we calculated the average velocity of the advancing fronts to be 117.4 ± 59.3µm/d (n=3). However, a remarkable feature of the invasion patterns is the distant dispersal of a small fraction of cells far away from the bulk of the invasive front at later time points (Fig. 2a). For instance, some of the more invasive cells are >1–2mm ahead of the leading edge of the invasive front at day 7 and many millimeters beyond the initial plug boundary (Fig. 2a), consistent with recent findings by us21 and others24, 25 on heterogeneously invasive subpopulations of carcinoma cells, and suggests that analysis of the distinct heterogeneous behavior of highly migratory cells may provide important insights into invasion dynamics that influence metastatic dissemination. Furthermore, the nonlinear nature of the front is typical of cancer cell invasion and reaction-diffusion models have been reported to explain such behavior in glioma26, 27. However, it is not well understood whether heterogeneity exists in the diffusive behavior of cells across the invasive front, which prompted us to probe the spatio-temporal variations in cell alignment and migration.
Cell and collagen morphology along the invasive front
At the onset of invasion, cells in the plug that have not encountered the anisotropic collagen are randomly oriented while cells at the invasive front interacting with aligned collagen, not surprisingly, tend to align along the direction of ECM alignment (Fig. 1e). Once robust invasion has developed, there are three distinct regions of interest at any given time point, namely the bulk region representing a segment of very high densities of cells that are within the advancing tumor boundary at its current location; the leading edge of the invasive front that is a 0.3–0.5mm region capturing the sharpest drop in cell density located at the transition from highly crowded to single dispersed cells (i.e., cells at the edge and just beyond the tumor boundary); and cells invading well beyond (>0.5mm) the leading edge of the invasive front (Fig. 3a). It is important to reiterate that taking into account the bulk region within the initial cell-dense plug, the shape of the invasion fronts in the early (Fig.1f) or the late stages (Fig. 2b, 3a) remains similar, and the transition from the former to the latter is associated with an expansion of the bulk region as the boundary of the tumor-like plug extends into the stroma-like collagen.
Fig. 3. Cell and collagen alignment at distinct regions of the invasive front.
(a) Typical cell intensity profile after 5 days of invasion into an aligned matrix with different regions identified by light pink demarcations: ‘Bulk’ (upper flat region), Leading ‘Edge’ (0.3–0.5mm region where the cell densities drop sharply to a minimum), and ‘Beyond edge’ (>0.5mm farther from the leading edge). (b) Fluorescence micrographs showing F-actin (red), nuclei (blue), and collagen (gray) morphology of typical sections in the defined regions of the invasive front. (c) Quantification of the degree of collagen and nuclear alignment in the three distinct regions of interest showing lower nuclear alignment in the bulk with a trend of increasing orientation in cells that have migrated farther from the bulk even as the collagen alignment remains largely the same throughout the construct (n=6–7 distinct positions for each group with 20–200 cells/position and >500 collagen fibers/position, ns=no significance, *p<0.05 using ANOVA and post-hoc multiple comparison testing).
To facilitate analysis of cell and collagen fiber alignment at various points in the developed front, we imaged stained cells and the matrix after several days of invasion using simultaneous MPE and SHG to visualize F-actin, nuclei and collagen fibers (Fig. 3b). Since it was difficult to delineate between individual cell boundaries in the densely packed bulk region, we employed nuclear orientation as a metric of cell alignment as has been previously done in several contact guidance studies28, 29. Using alignment indices that we described previously21, we quantified the bias in cell orientation and surrounding ECM anisotropy at different locations along the invasion front and at distant regions beyond the front. Not surprisingly, collagen fiber alignment index is largely constant throughout the entirety of the invasive front, which is consistent with the objective of the assay to provide a largely uniform aligned ECM for carcinoma cell invasion (Fig. 3a, b). However, while cells in all regions display some bias in orientation due the response to contact guidance, cells at and beyond the edge of the invasive front show a greater degree of orientation in the direction of ECM alignment. When examining regions beyond the leading edge of the invasive front, it is clear that cells in that zone should behave like sparsely populated single cells in an aligned collagen matrix, a behavior we have extensively characterized previously using MDA-MB-231 cells21. Consistent with our previous work11, 21, carcinoma cells beyond the leading edge are highly aligned to the direction of collagen alignment (Fig. 3b, c). Likewise, at the leading edge of the invasive front, carcinoma cells are also highly oriented even though the cell density is substantially higher (Fig. 3b, c). This is certainly in agreement with the contact guidance response of single carcinoma cells, and those that have undergone an epithelial-to-mesenchymal transition and therefore do not form strong force-transmitting cell-cell junctions that can compete with ECM guidance cues, even when higher cell densities result in adjacent placement of these cells11. However, at the bulk region of the invasive front, while cells remain aligned, the degree of alignment is significantly less, even as the underlying matrix remained equally anisotropic (Fig. 3b, c). This is most likely due to crowding and cell-cell interactions at the very high cell densities, with a number of cells growing on top of each other at these locations, thereby diminishing responsiveness to the underlying matrix architecture. Indeed, evidence of cells stacking on top of each other to generate cell layers >100µm thick can be observed from 3D reconstructions of the invasive front in the aligned matrix at later time points (Supplementary Fig. 2c, e). Therefore, there may be cell density-dependent spatial variations in contact guidance-directed invasion along the front.
Spatio-temporal variations in carcinoma cell invasion dynamics
In order to gain insight into the dynamics of anisotropic stromal invasion by carcinoma cells from a confined lesion, we investigated the migration dynamics of invading cells at different locations of the front at various time points. As discussed above, the developing invasive front at early time points is comprised of cells within the bulk tumor boundary embedded in isotropic ECM and pioneer invading cells at the leading edge interacting with aligned collagen. In the mature front, however, both the bulk and leading edge of the invasive front regions encounter the anisotropic matrix. To study 3D cell migration behavior, we utilized time lapse two-photon microscopy of migrating cells in the engineered construct and analyzed their movement by fitting cell trajectories to a persistent random walk model along each axis, which enables comparison of parameters of cell migration between the orthogonal directions30, 31. Owing to the complexity of 3D tracking of densely packed cells and our previous work21 demonstrating that ~90% of the motility of single MDA-MB-231 cells migrating through aligned collagen matrices is confined to the XY plane, we analyze and present data from projected tracks on the XY plane, i.e., from 2D cell tracking (Supplementary Movie 2, 3).
Cell dispersal, as expected, is largely anisotropic due the well-defined aligned ECM tracks. The directionality of migration, which is the percentage of total motility directed along a given axis21, is significantly higher for cells in regions with anisotropic collagen, viz. the leading edge of the developing invasive front and both the bulk and leading edge of the mature front (Fig. 4a, b). Note that cells behind the leading edge (bulk) in a developing front are still within the initial tumor-plug boundary and have yet to encounter the aligned collagen and that is certainly reflected in their directionality of migration (Fig. 4a, b). Moreover, the cells at the leading edge in the mature front are significantly more directional than the pioneer invading cells in the developing front that appear at the plug boundary in the initial stages of invasion (Fig. 4a, b). While the latter group of cells do exhibit directional movement, the isotropic forces exerted on the local matrix by the cell-dense plug behind them is likely a counteracting factor.
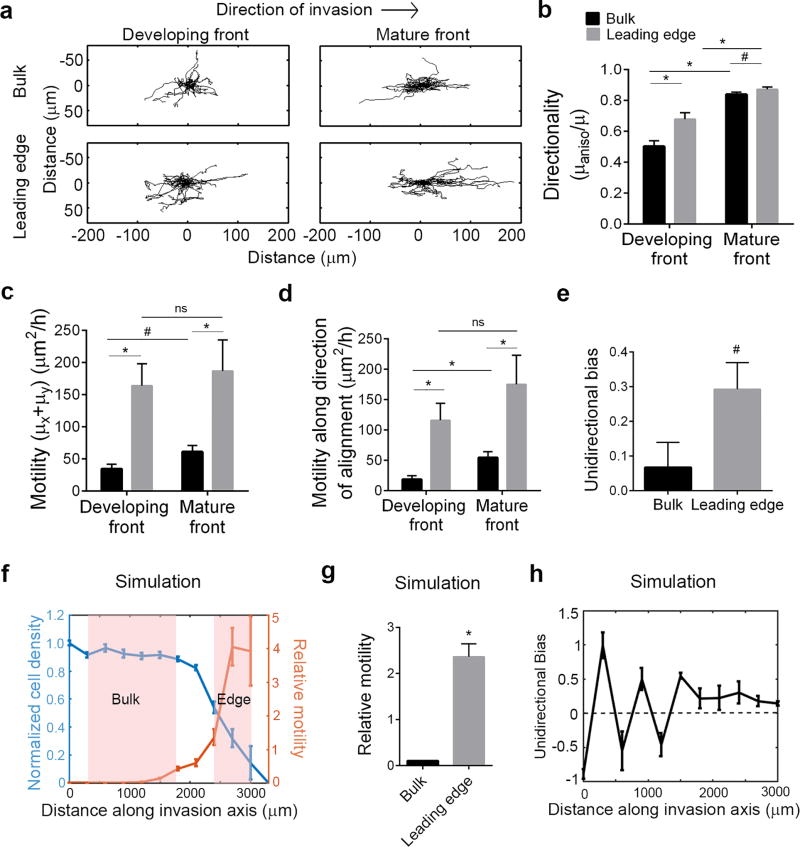
Fig. 4. Spatio-temporal variations of cell invasion.
(a) Trajectory plots showing migration behavior of MDA-MB-231 cells in the bulk region and at the leading edge of an early (developing) or a fully developed (mature) front. Comparison of (b) directionality of migration, (c) total motility, (d) motility along the direction of alignment for the corresponding groups demonstrating increased motility and directionality of cells at the leading edge compared to the bulk. (e) Unidirectional bias of cell migration showing cells at the leading edge of a mature front more frequently migrate in the direction of invasion than cells within the bulk. (f) Normalized cell density profiles from Brownian dynamics simulations of invading cells showing the characteristic invasion front, where bulk and leading edge regions can be defined (demarcated in pink), and corresponding spatial variation in one-dimensional motility of cells relative to the input motility. (g) Simulated motility of cells normalized to the input motility showing an enhanced migration of cells at the edge compared to the bulk due to synergy between growth and migration, and suppressed migration in the bulk due to inhibition from cell crowding or “jamming”. (h) Profile of unidirectional bias of migrating cells as a function of location along the front showing large fluctuations in the bulk settling into uniformly positive bias (in the direction of invasion) at the leading edge (for b-e: n=40–70 cells/group, ns=no significance, *p<0.001, #p<0.05, unpaired Mann Whitney test; for g: n>120/group, *p<0.001 by unpaired t-test). Data in b-h are mean ± SEM.
Interestingly, both in the developing and mature fronts, cell motility at the leading edge is greater than that in the bulk (Fig. 4a, c, Supplementary Movie 2, 3). The increase in total motility at the edge over the bulk is also mirrored by the enhanced motility along the direction of alignment (Fig. 4d). The enhanced motility observed in a persistent random walk may be due to increases in either speed or persistence time, or both. In this case, the differences in motility between the leading edge and bulk are largely due to changes in speed along the direction of alignment, while the persistence times are less variable (Supplementary Fig. 3a, b). There is, however, a significant difference in persistence between cells in the bulk and leading edge of the developing front, likely owing to the differences in underlying matrix alignment, as well as a trend (p<0.06) of increased persistence times in the mature front (Supplementary Fig. 3b). Moreover, it is important to note that along the direction of ECM anisotropy, both the speed and persistence times for all the individual groups are respectively higher than those in the orthogonal direction (Supplementary Fig. 3a-d). Apart from cells in the bulk of the developing front that show largely random movement and comparable numbers between the speeds and persistence times along the orthogonal axes, up to 50% greater speed and persistence times are present along the direction of alignment for the other three groups (Supplementary Fig. 3a-d). This is certainly congruent with the finding that in an anisotropic matrix, the majority of total cell motility (~70%) is directed along the orientation of the ECM fibers21.
Another remarkable feature of the spatial variation in migration of cells during invasion can be observed by studying the trajectories of cells at the leading edge versus the bulk of a mature front. While the directionality is significantly, yet modestly, different between the groups (Fig. 4b), the cells at the leading edge tend to move in a unidirectional fashion, i.e., away from the interface while those in the bulk show bidirectional migration (Fig. 4a,e, Supplementary Movie 2, 3). This is quantitatively captured using the ratio of the total step-wise displacement of each cell along the invasion axis to the total step-wise distance (unsigned displacement) covered to metricize unidirectional bias. This ratio would assume a value of -1 for cells moving perfectly towards the interface, 0 for bidirectional cells and 1 for cells moving perfectly in the direction of invasion. We note that while both groups on average have positive unidirectional bias, it is significantly higher for cells at the leading edge compared to those in the bulk (Fig. 4e). In other words, regions in the bulk surrounded by high density of cells on both ends do not as effectively “perceive” differences in their environment with one side largely appearing the same as the other.
Overall, the preceding results confirm and characterize the effect of contact guidance due to the aligned collagen fibers as a strong local regulating factor in the dynamics of cell migration during invasion. However, contact guidance alone is insufficient to fully explain why the cells at the leading edge tend to move faster and more frequently in the direction of invasion than the cells in the bulk. We postulated that such differences could be explained simply by considering the enhanced crowding of cells in the bulk and its influence on cell movement by contact inhibition32. To test this hypothesis, we employed a Brownian dynamics simulation for cell proliferation and migration with single cell values of cell motility and growth obtained from published experimental data by us21 and others (NIH Physical Sciences in Oncology Network Bioresource Core Facility, Protocol NCI-PBCF-HTB26). In the simulation, cells are allowed to grow, divide, and migrate while maintaining non-overlapping boundaries along a one-dimensional track, mimicking guided invasion along the direction of collagen alignment. Previously, it was shown that under some conditions the model predicts the existence of a “jammed” state, where an advancing front of tumor cells is propelled quasi-ballistically through synergistic interaction between proliferation and migration, an effect not captured with reaction-diffusion models using realistic single cell migration speeds33. Over several days, the simulated cells dispersing along the invasion axis produce a similar cell density versus distance curve as observed experimentally in mature invasion fronts with clearly distinguishable bulk and leading edge regions (Fig. 4f). Indeed, the model predicts that the motility of cells increases dramatically along the front from the crowded bulk region to the leading edge, where cells have free space to allow for largely unhindered migration (Fig. 4f). Consistent with the experimental data, the free leading edge cells thus display a significantly higher motility than those in the bulk (Fig. 4f, g). In addition, unidirectional bias for the simulated cells in the bulk is highly variable, spanning both positive and negative values but settled to a positive value of ~0.25 at the leading edge (Fig. 4h). Therefore, cells at the leading edge, owing to the unoccupied space available for migration in the direction of invasion, display a consistent positive unidirectional bias, in agreement with our experimental results (Fig. 4e, g, h). Thus, in addition to contact guidance, physical contact inhibition, manifested as a crowded state, plays an important role in the invasion dynamics observed here. Furthermore, it is important to note the key difference from a purely diffusive dispersal, where the fundamental input growth and movement parameters of individual cells in high and low density regions is assumed to be independent of their concentration or of position. Overall, our experimental and simulation results suggest that the phenomenon of physical crowding acts in concert with random diffusive behavior leading to the emergent invasion into less populated regions from an overgrown lesion when a physical barrier is not in place to constrain cell distribution. Indeed, our combined experimental and modeling results demonstrate the lack of uniformity in migration both spatially and temporally during invasion, where local cues dominated by contact guidance and physical contact inhibition together contribute to the emergence of the advancing invasion front.
Discussion
While great insight into cancer cell migration can be obtained from 2D systems, 3D culture systems of increasing complexity are desirable to investigate fundamental processes in a more in vivo-like environment. In particular, since work over the past decade has undoubtedly established the importance of contact guidance in tumor cell invasion, e.g. 6, 8, 11–15, 21, 34–38, a concomitant need for more advanced 3D models that incorporate tumor-relevant ECM structural anisotropy has emerged in order to study the mechanisms of invasion and 3D migration processes in greater and more physiologic detail. In this study, we have taken a step in this direction. Building on our previously described method of generating aligned 3D collagen matrices, we introduce an engineered and accessible system to probe the dynamics of carcinoma cell invasion from a confined lesion into anisotropic stromal collagen. While our method in principle is quite simple and tractable, its implementation poses some interesting nuances. The inherent differences in the structure of different aligned gel constructs, the somewhat empirical assessment of the initial air-drying period, and variation in quality of the interfaces create some assay variability, which may indeed help capture some of the heterogeneity observed in vivo. Such variability, however, could be in all likelihood reduced by integrating the whole setup into a single device in next generation platforms. Furthermore, with the evolution of the invasive front and proliferation of cells over several days, we observed a significant compaction of the cell-dense plug, particularly at and near the interface and also in the bulk of the aligned matrix (Supplementary Fig. 2a, c, e). This, along with extensive matrix reorganization associated with a massive quantity of cells close to the interface can at times make it challenging to image and delineate the exact location of the interface at later time points. Likewise, another associated feature owing to differences in the interface formation was the non-uniformity in the initial invasion time, i.e., in some experiments it took longer for the cells to start to invade through the interface. Nevertheless, one could still calculate the invasion rate by imaging the fronts sequentially over time after the cells have encroached into the stroma. Lastly, one of the unique features of our design, namely the fact that it interfaces a pre-made matrix with a newly forming one, opens up the possibility of pre-treating or perturbing either matrix together or independently to generate different stromal interfaces suited for specific applications, such as stiffening by glycation39, 40, altered ECM compositions, co-culturing with stromal cells etc.. While we have demonstrated that our assay works for two different ECM plug components, in theory the general principle could be extended to generate homotypic or heterotypic 3D interfaces between any two hydrophilic ECM components. Thus, this engineered 3D platform provides a unique window into carcinoma invasion into reorganized stromal collagen that enables imaging and analysis of the initial intrusion into the aligned matrix, the evolution of the invasion front, and migration of individual cells as well as molecular probing at the single cell level at any time point.
While several studies to date have studied advancing invasion fronts of cancer cells in isotropic matrices41, 42, this is, to our knowledge, the first study to analyze these patterns in a 3D anisotropic matrix. Comparing our results to limited in vivo data from brain cancers and renal cell carcinomas, our calculation of the front velocity was roughly an order of magnitude higher than in vivo tumor growth rates there were measured in mm/yr 43, 44. This is not surprising and may be a combination of a number of factors including nonlinear spatial and temporal changes in the in vivo tumors, the inherent resistance to tumor expansion and dissemination within a living tissue, the more complex ECM structure and composition in vivo, the distinct underlying genetics between the systems, and/or the highly invasive cell line used here, etc. However, the shapes of the invasion fronts were remarkably consistent and our ability to track the evolving fronts over many days makes this assay amenable to testing of pharmacological interventions and mathematical modeling of disease progression. Apart from the general shape of the invasive front, the outlier cells disseminated far away from the bulk are also worthy of special attention since these are perhaps the cells that most effectively escape to seed ectopic sites, and may represent cells with increased stem-like properties21. Interestingly, these outlier cells do not appear in the simulated invasion fronts in which the same input motility was used for the whole population, suggesting that directed migration for these cells is being dominated by the contact guidance cues and that they may represent cells with enhanced motility, such as the stem-like subpopulation21. Further, these cells also have an increased likelihood of not being captured during a tumor resection and could thus continue to contribute to seeding metastases or pioneering the recurrence of disease. Certainly, therapeutic interventions that specifically eliminate these robustly advancing cells are needed.
Comparing the characteristics of MDA-MB-231 cell movement in the invading fronts to the sparse single cell migration in aligned 3D matrices we previously reported21, we found that the total motility as well as the motility and speed along the fiber alignment axis in the invasive front were lower here than previously observed for single cells (Fig. 4c, d, Supplementary Fig. 3a). Interestingly, imaging collagen structure confirmed that the fiber density was much higher in the stromal collagen encountered by the cells here than in the unmodified aligned constructs alone, due to the decreased thickness of the matrix perhaps owing to the partial drying of the pre-aligned matrix before attachment to the tumor plug. Thus, cells invading through the matrix in this platform encounter a more restrictive and challenging 3D environment, perhaps more closely mimicking native in vivo ECM than those in the unmodified aligned matrices, which in part explains their reduced motility and speed. Reduced motility may also be induced partly by the high cell density and distinct chemical gradient in this assay as compared to our previous observations21.
Lastly, tracking the evolving invasion fronts over time and quantification of their shapes allowed us to identify distinct regions of interest in the experimental and simulated invasion fronts. Since the majority of single cell migration in the pre-aligned matrix was directed along the axis of alignment, we were able to model aspects of the invasion with a one-dimensional Brownian dynamics simulator. While the model does predict the enhanced magnitude and unidirectional bias of motility at the advancing edge versus the bulk region, the differences, especially in the magnitude of motility, are larger than the experimental data (Fig. 4d, g). This can be explained, at least in part, by the stringency of non-overlapping cells in the model whereas in the experimental setting we do find cells stacked on top of each other creating cell layers many cell diameters thick in regions of high density. Experimentally, the leading edge cells in the invasive front at the onset of invasion, comprised of single pioneer probing cells, were found to be less directional guided than those at the edge of a mature front suggesting that collective single cell streaming may be a more efficient mode of directional migration than single cell dissemination in this region. Similarly, in the invasive front edge a combined effect of contact guidance and contact inhibition is demonstrated by the difference in motility between bulk cells during early and late invasion (Fig. 4a, c). Clearly, these are both densely populated regions within the tumor boundary, but the surrounding matrix architecture is different. It can be hypothesized that cells within the mature bulk region, by virtue of their elongation and concerted movement along the direction of collagen alignment, experience less crowding and consequently higher motility than the cells in the initial plug with the same density. However, in the current simulations, such differences in cell shape and size or cell-cell interactions (apart from physical exclusion) were not incorporated. Other compelling questions may also be raised in this context, such as the relative role of cell growth and motility, both of which are dysregulated in malignant disease, as drivers of stromal invasion of carcinomas and how these dynamic processes may evolve over time. Further iterative experimental and modeling studies, particularly with simulations using full 3D models that are more computationally demanding, to dissect these components of disease progression will certainly add insight to our understanding of these phenomena in metastatic disease. Nevertheless, the model employed here does predict the experimental observations with regards to the differences in invasive behaviors at the leading edge of invasion versus the bulk. Such spatial variations emphasize that the entire front does not simply translate through the matrix as a whole, but instead the movement of the front is an emergent behavior arising from complex dynamics of individual cells growing, dividing, and migrating in their microenvironment, with some cells largely de-coupled from these processes as they have advanced great distances into the ECM. This raises ever more interesting questions on how to specifically target cooperating behaviors for heterogeneous cells and disparate cell types in distinct microenvironments. Certainly, our complex experimental platform combined with mathematical-computational modeling could help parse out these complex interactions and provide a valuable tool to answer fundamental questions and explore and understand interactions between critical processes in cancer progression.
Materials and Methods
Cell culture
Validated MDA-MB-231 cells were freshly obtained from ATCC (2013) and used at low passage relative to the original culture. Cells were grown in high glucose DMEM (HyClone) supplemented with 10% fetal bovine serum (FBS; HyClone). Stable GFP expression was induced in MDA-MB-231 cells using GFP-lentivirus particles (Gentarget) and subsequent positive selection using puromycin (Invivogen). Primary breast cancer cells and primary carcinoma-associated fibroblasts were derived from invasive mammary carcinomas from MMTV-PyMT mice as described45 using differential trypsinization and selective outgrowth. These cell lines were grown and maintained in DMEM supplemented with 10% Fetal Bovine Serum (FBS). All animal work was approved by the University of Minnesota Institutional Animal Care and Use Committee (IACUC) and all animal and experimental work followed institutional and NIH guidelines.
Fabrication of aligned collagen matrices
Aligned collagen matrices were generated as previously described21. Briefly, 3mg/ml collagen matrices seeded with mammary carcinoma-associated fibroblasts were prepared in a modified 6-well plate to form rectangular constructs connected at the long ends to a pair of porous polyethylene anchors. Following overnight incubation, the matrices were detached from the bottom of the plate and incubated for an additional 1–2 days while attached only to the anchors at its two ends. Fibroblast-mediated contraction during this time compacts the construct into a dog-bone shape with concomitant collagen fiber alignment along the axis joining the two anchors. Subsequently, these matrices are decellularized using a two-step cell lysis and nuclease treatment protocol and stored at 4°C until further use. High-density rat tail collagen-I (Corning) (purity of >90%, according to the manufacturer’s specifications) was used as the collagen stock and polymerized by neutralizing in HEPES buffer solution, as previously described8, 21. Note that since the aligned constructs are generated by compaction of the original gel, the final density can be higher than the starting density of 3mg/ml, as is the case for any compacted matrix (isotropic, anisotropic etc.). The thickness of these anisotropic, decellularized constructs was measured by calipers while maintaining the gel flat in a bath of PBS by clamping the polyethylene spacers at the two ends of the gel onto the opposite arms of a uniaxial stretcher.
Constructing the 3D invasion assay
First, 4mL of 1.5–2% agarose in 1X Tris-buffered saline was poured onto a 35mm tissue culture dish and let solidify to form a uniform layer on the plate. This cylindrical layer of agarose was then cut along a straight line ~1.5–2cm from the edge of the plate with a scalpel blade and the larger portion removed. The remaining portion provides a straight barrier against which the plug can be pipetted while keeping the plate tilted and retaining lower height as compared to the walls of the plate to provide better access to a microscope objective for imaging. Next, a small piece of Parafilm “M” laboratory film (Bemis) ~1.5 cm in width is cut out and fixed onto the plate and onto the directly adjacent agarose layer. Then an aligned collagen matrix, generated as described above21, is detached from its two polyethylene anchors (Interstate) and placed carefully with its long axis perpendicular to the agarose barrier and one end of it overhanging marginally onto the piece of Parafilm. The two polyethylene anchors were then glued on either side of the short axis of the aligned matrix near the agarose layer as hydrophobic barriers (See Fig. 1d). In theory, any hydrophobic solid material such as PDMS could be utilized as barriers. This creates a small rectangular Parafilm-coated region bounded by the agarose and barriers on three sides and the overhang of the pre-aligned matrix on the other. The setup was left to air dry for several minutes while preparing the cell-seeded collagen plug.
To prepare a cell-seeded collagen plug, high-density rat tail collagen (Corning) was neutralized by a HEPES buffer and cells in suspension were mixed with it to achieve a final concentration of 4mg/ml collagen with 6.7 X 106 cells/ml. The matrix was allowed to start polymerizing for 6–7mins before 75µl of this collagen mixture was pipetted into the rectangular nook at the edge of the aligned matrix, making sure the edge just overlapped with the pipetted plug. While pipetting the plug, the plate was maintained in a tilted position at an angle of ~30° (usually done by balancing it against the lid of a 50ml conical tube or a 35mm plate) so that gravity can counteract the forces from surface tension that may cause the plug to spill over to the bulk of the aligned matrix as it is polymerizing. The gel was allowed to polymerize for 15mins further at room temperature before moving the setup to a 37°C incubator in a humidified chamber maintaining the slanted position. After another 1.5h, a small amount of media was carefully added to soak the pre-aligned matrix, not disturbing the polymerizing plug, and incubated overnight in the humidified chamber for the matrix to fully polymerize. The next day, the assay was fed with cell culture media and henceforth incubated in a flat position without the need for a humidified chamber. Subsequently, within a day or two, the plug was detached from the barriers and subsequently contracts away from them, integrating into the aligned matrix as one single piece of tissue. This could then be removed from the entire setup and placed by itself in a 35mm tissue culture plate for subsequent invasion.
In order to prepare cell-seeded Matrigel plugs, the same number of primary mammary carcinoma cells were mixed with growth factor reduced Matrigel (Corning) to a final concentration of 5mg/ml and the same 75µl total volume of the plug was interfaced with the aligned matrix. Due to the quick gelling properties of this matrix, the plate was removed from the tilted configuration and the humidified chamber and complete growth media added to it after 1.5h.
Imaging and analysis of invasive fronts
Invading carcinoma cells and surrounding collagen architectures were visualized using combined MPE and SHG imaging on a custom-built multi-photon laser scanning microscope 46 (Prairie Technologies / Bruker) using a Mai Tai Ti:Sapphire laser (Spectra-Physics) at an excitation wavelength of 880nm. Multi-dimensional image acquisition involving Z-stacks at several adjacent fields of view starting from the interface to beyond the leading edge of the invasive front were captured, merged together and then projected along different axes (Fiji) to obtain the XY and XZ views shown in Figs. 1, 2, and Supplementary Fig. 2. Distinct changes in collagen density and structure were utilized to mark the location of the interface. The thickness of the cell and collagen layers were calculated by image analysis in Matlab by determining the width of the major peak (beyond a noise threshold) in intensity along each column of pixels. Data were smoothed by a moving average over 100 pixels to obtain profiles shown in Supplementary Fig. 2. Fractional overlap was calculated by dividing the thickness of the portion of the cell layer overlapping with the collagen layer by the total thickness of the cell layer.
From the XY projected images, average intensity profiles were measured along the X axis as a relative measure of cell density at each location (Fiji). The raw data was converted to a relative intensity scale, smoothened by moving averages and fitted to Gaussian curves centered at the interface (Matlab). The half-width at half maximum of the fitted Gaussian was taken to represent the distance of the corresponding front from the interface. If σ denotes the standard deviation of the fitted Gaussian, then the distance of the front from the interface was thus given by
| (1) |
This distance obtained from multiple measurements of an advancing front was used to calculate its average velocity.
Immunofluorescence staining and quantification of morphology
The plug and adjoining aligned matrix were fixed in 4% paraformaldehyde (Sigma) for 20mins, permeabilized with 0.1% Triton X-100 (Roche), quenched in 0.15M glycine (Sigma) for 10mins and blocked with a solution of 2% fatty acid free-BSA (Fisher Scientific) + 2.5% goat serum (Sigma), followed by incubation with rhodamine phalloidin (1:250; Life Technologies) and 1:40000 bisbenzamide (Sigma). Imaging was subsequently performed using multiphoton laser scanning microscopy to visualize F-actin, nuclei and collagen. The leading edge was defined as positions where the field of view contained partially confluent invading cells, whereas the bulk region was defined as a location in between the interface and invasive front, usually ~600–1000µm behind the leading edge of the invasive front with spatially invariant cell density.
Automated quantification of nuclear morphology was done using CellProfiler47, with subsequent analysis in Matlab. Collagen fiber analysis and quantification of nuclear and collagen alignment indices were performed as previously described21. If σ denotes the standard deviation of a distribution of collagen fiber orientations, ranging from -90 to 90, 0 being the direction along the anisotropic axis, the alignment index is then given by
| (2) |
where the numerator denotes the standard deviation for a uniform distribution with the same range.
Live cell timelapse imaging and cell migration analysis
Live cell imaging of cell migration using simultaneous MPE of fluorescently labeled cells and SHG imaging of surrounding collagen fibers, was performed as described previously21. Briefly, cell migration was captured by taking 2-channel Z stacks of at 5–10µm intervals at each stage position at 20min intervals over 12–16h for cells in the bulk and the leading edge of a developing (early) or mature (late, 4–7 days after initial intrusion through the interface) invasion front in a custom temperature controlled chamber21. The definitions of the invasive front and bulk were the same as noted above.
For cell migration analysis, only the maximum intensity projection data on the XY plane were considered. 2D tracking of cell migration was performed after registration of stacks (StackReg48, Fiji) using the Manual Tracking plugin (Fiji). The method of overlapping intervals49 was used to fit the cell trajectories to a persistent random walk model (PRWM)30, 31 using Matlab (Mathworks) to interface with the cell tracking output, as described previously21. Mathematically, the PRWM can be written as
| (4) |
where MSD denotes the mean squared displacement, S is the migration speed, P is the persistence time, and nd is the dimensionality of the random walk.. The motility coefficient is given as
| (5) |
We fit the model separately to the two orthogonal directions of motion, thus obtaining motility, speed and persistence times for×and y directions (therefore, nd =1 in each case). Directionality of migration along any given axis was obtained by simply taking the ratio of the motility along that axis to the total motility of the cell, thus quantifying the fraction of total motility that is directed along that particular axis21.
To capture the tendency of leading edge cells to move more often in the direction of invasion, we used a metric called unidirectional bias. For each cell track, this was simply the ratio of the sum of all piece-wise displacements along the direction of invasion to the sum of all piece-wise distances covered along the same direction. Thus, if at each time step i, the movement of a cell along the direction of invasion is xi, then its unidirectional bias would be given by
| (6) |
In our setup, positive values of xi denotes movement in the direction of alignment. Thus, this metric assumes values of -1 (perfect unidirectional movement away from the direction of invasion), 0 (unbiased bidirectional migration) and +1 (perfect unidirectional movement towards the direction of invasion) for three distinct cases.
Brownian Dynamics Simulation of cancer cell invasion
A Brownian Dynamics Tumor Simulator that accounts for both cell proliferation and migration was adapted from previously published work50 to test the hypothesis that physical crowding of cells influences the spatial variability in migration along the invasion front observed in our experiments. In the model, each cell is treated as a sphere with a starting diameter of 20µm and allowed to move one-dimensionally via Gaussian-distributed steps dictated by a random motility coefficient51 of 5µm2/min, which is of the same order of magnitude as our previous experimentally derived value of average single cell motility for MDA-MB-231 cells21. In addition, each cell was also allowed to grow and divide with a proliferation rate (1/day), obtained from publicly available data characterizing behavior of MDA-MB-231 cells.
Beginning with an initial value of 1min, time intervals were set such that each time interval was divided into equal timesteps dictated by the number of present cells at that instant, as previously described33. At each timestep, a cell was selected from a uniform probability distribution function among the entire pool of cells, and either underwent movement in the form of random walk diffusion, growth, or both to the extent calculated for the length of the time interval. Importantly, only those movements would be allowed which do not lead to physical overlap among cells, thus simulating an idealized case of physical contact avoidance. Twenty initial cells with varying initial volume (correlated with the state of growth, imposes an asynchronous point in the cell cycle across the initial cells) were spaced uniformly 80µm away from each other centroid to centroid, and the entire simulated time was set to be seven days. During this timespan, cells were allowed to proliferate, divide, and move, hence occupy more space and exhibit a crowding effect that initiates a physical contact inhibition or jammed state in which the leading edge of the cell ensemble exhibits a linear advancement through time instead of a random walk’s purely diffusive behavior, i.e. becomes quasi-ballistic. We limited our analysis to a timespan in this crowded state, preceding the completely jammed configuration. In this timespan, the spatial distribution of cells resembled the experimental invasion fronts in that they could be divided into distinct bulk and leading edge regions, as defined previously.
For data analysis, the simulated values were sampled once every 100 timesteps, which amounted to a duration ranging from 83 to 93 mins and an average of 89 mins. We calculated the MSD of cells in that time period in the crowded regime by the method of overlapping intervals and subsequently obtained the motility coefficient by the slope of the MSD versus time curve. The axis of invasion was divided into 300µm segments (which were approximately the same as our field of view during live cell imaging experiments) and the motility of all cells within each segment was grouped together. For calculating unidirectional bias, similar segmentation was used. However, in the latter case, the total movement of all cells within a given segment were taken together to calculate the unidirectional bias of cells within that segment. The invasion front was divided into bulk and leading edge sections based on the cell density versus distance along the invasion axis curve according to definitions mentioned above. Results from 12 independent simulations were combined to obtain the reported data.
Statistical Analysis
Student’s t test was used to compare null hypotheses between two groups for large datasets. The non-parametric Mann Whitney test was employed for non-normal or small datasets. Multiple groups were compared by ANOVA and post-hoc tests. Unless otherwise mentioned, the data analyzed were pooled from many cells/field of view over several fields of view across n≥2 experiments. Number of data points for each group, the specific statistical tests, and significance levels are noted in the figure text.
Supplementary Material
Acknowledgments
PPP and this work was supported by a Research Scholar Grant, RSG-14-171-01-CSM from the American Cancer Society. This work was also supported by the NIH (R01CA181385 to PPP, R01CA172986 to DJO, and U54CA210190 University of Minnesota Physical Sciences in Oncology Center to PPP and DJO), UMN College of Science and Engineering (PPP) and Masonic Cancer Center (PPP), and grants from the UMN Institute for Engineering in Medicine (PPP), and the Randy Shaver Research and Community Fund (PPP). AR was supported by a UMN Doctoral Dissertation Fellowship. RKM is support by a NSF graduate research fellowship 00039202. The content of this work is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or other funding agencies. We thank members of the Provenzano laboratory for insightful comments regarding this work.
Footnotes
Conflicts of interest
There are no conflicts of interest to declare.
References
- 1.Roussos ET, Condeelis JS, Patsialou A. Nat Rev Cancer. 2011;11:573–587. doi: 10.1038/nrc3078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Charras G, Sahai E. Nature Reviews Molecular Cell Biology. 2014;15:813–824. doi: 10.1038/nrm3897. [DOI] [PubMed] [Google Scholar]
- 3.Friedl P, Alexander S. Cell. 2011;147:992–1009. doi: 10.1016/j.cell.2011.11.016. [DOI] [PubMed] [Google Scholar]
- 4.Kim DH, Provenzano PP, Smith CL, Levchenko A. J Cell Biol. 2012;197:351–360. doi: 10.1083/jcb.201108062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Provenzano PP, Eliceiri KW, Keely PJ. Trends in cell biology. 2009;19:638–648. doi: 10.1016/j.tcb.2009.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Provenzano PP, Eliceiri KW, Campbell JM, Inman DR, White JG, Keely PJ. BMC Med. 2006;4:38. doi: 10.1186/1741-7015-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Conklin MW, Eickhoff JC, Riching KM, Pehlke CA, Eliceiri KW, Provenzano PP, Friedl A, Keely PJ. Am J Pathol. 2011;178:1221–1232. doi: 10.1016/j.ajpath.2010.11.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Provenzano PP, Inman DR, Eliceiri KW, Trier SM, Keely PJ. Biophysical journal. 2008;95:5374–5384. doi: 10.1529/biophysj.108.133116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bellail AC, Hunter SB, Brat DJ, Tan C, Van Meir EG. The international journal of biochemistry & cell biology. 2004;36:1046–1069. doi: 10.1016/j.biocel.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 10.Drifka CR, Tod J, Loeffler AG, Liu Y, Thomas GJ, Eliceiri KW, Kao WJ. Mod Pathol. 2015;28:1470–1480. doi: 10.1038/modpathol.2015.97. [DOI] [PubMed] [Google Scholar]
- 11.Ray A, Lee O, Win Z, Edwards RM, Alford PW, Kim DH, Provenzano PP. Nat Commun. 2017;8:14923. doi: 10.1038/ncomms14923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee M, Downes A, Chau YY, Serrels B, Hastie N, Elfick A, Brunton V, Frame M, Serrels A. Intravital. 2015;4 doi: 10.1080/21659087.2015.1055430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weigelin B, Bakker G-J, Friedl P. Intravital. 2012 doi: 10.4161/intv.21223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang W, Wyckoff JB, Frohlich VC, Oleynikov Y, Huttelmaier S, Zavadil J, Cermak L, Bottinger EP, Singer RH, White JG, Segall JE, Condeelis JS. Cancer research. 2002;62:6278–6288. [PubMed] [Google Scholar]
- 15.Beerling E, Oosterom I, Voest E, Lolkema M, Rheenen Jv. Intravital. 2016 doi: 10.1080/21659087.2016.1261773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grinnell F, Rocha LB, Iucu C, Rhee S, Jiang H. Exp Cell Res. 2006;312:86–94. doi: 10.1016/j.yexcr.2005.10.001. [DOI] [PubMed] [Google Scholar]
- 17.Miron-Mendoza M, Seemann J, Grinnell F. 2008 doi: 10.1091/mbc.E07-09-0930. [DOI] [Google Scholar]
- 18.Karamichos D, U. o. T. S. M. C. Department of Ophthalmology, Dallas, Texas, N. Lakshman, U. o. T. S. M. C. Department of Ophthalmology, Dallas, Texas, W. M. Petroll, U. o. T. S. M. C. Department of Ophthalmology, Dallas, Texas and S. M. C. Department of Ophthalmology, 5323 Harry Hines Blvd., Dallas, Texas 75390-9057, USA Cytoskeleton. 2017;66:1–9. [Google Scholar]
- 19.Carey SP, Starchenko A, McGregor AL, Reinhart-King CA. Clinical & experimental metastasis. 2013;30:615–630. doi: 10.1007/s10585-013-9565-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Beck JN, Singh A, Rothenberg AR, Elisseeff JH, Ewald AJ. Biomaterials. 2013;34:9486–9495. doi: 10.1016/j.biomaterials.2013.08.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ray A, Slama ZM, Morford RK, Madden SA, Provenzano PP. Biophys J. 2017;112:1023–1036. doi: 10.1016/j.bpj.2017.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Provenzano PP, Inman DR, Eliceiri KW, Keely PJ. Oncogene. 2009;28:4326–4343. doi: 10.1038/onc.2009.299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bredfeldt JS, Liu Y, Pehlke CA, Conklin MW, Szulczewski JM, Inman DR, Keely PJ, Nowak RD, Mackie TR, Eliceiri KW. J Biomed Opt. 2014;19:16007. doi: 10.1117/1.JBO.19.1.016007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cheung KJ, Gabrielson E, Werb Z, Ewald AJ. Cell. 2013;155:1639–1651. doi: 10.1016/j.cell.2013.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Konen J, Summerbell E, Dwivedi B, Galior K, Hou Y, Rusnak L, Chen A, Saltz J, Zhou W, Boise LH, Vertino P, Cooper L, Salaita K, Kowalski J, Marcus AI. Nat Commun. 2017;8:15078. doi: 10.1038/ncomms15078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Massey SC, Assanah MC, Lopez KA, Canoll P, Swanson KR. J R Soc Interface. 2012;9:1757–1766. doi: 10.1098/rsif.2012.0030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Swanson KR, Alvord EC, Murray JD. Br J Cancer. 2002;86:14–18. doi: 10.1038/sj.bjc.6600021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dunn GA, Ebendal T. Exp Cell Res. 1978;111:475–479. doi: 10.1016/0014-4827(78)90196-9. [DOI] [PubMed] [Google Scholar]
- 29.Manwaring ME, Walsh JF, Tresco PA. Biomaterials. 2004;25:3631–3638. doi: 10.1016/j.biomaterials.2003.10.043. [DOI] [PubMed] [Google Scholar]
- 30.Othmer HG, Dunbar SR, Alt W. Journal of mathematical biology. 1988;26:263–298. doi: 10.1007/BF00277392. [DOI] [PubMed] [Google Scholar]
- 31.Harms BD, Bassi GM, Horwitz AR, Lauffenburger DA. Biophys J. 2005;88:1479–1488. doi: 10.1529/biophysj.104.047365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Carmona-Fontaine C, Matthews HK, Kuriyama S, Moreno M, Dunn GA, Parsons M, Stern CD, Mayor R. Nature. 2008;456:957–961. doi: 10.1038/nature07441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Klank RL, Rosenfeld SR, Odde DJ. Convergent Science Physical Oncology. doi: 10.1088/2057-1739/aa9e6e. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Goetz JG, Minguet S, Navarro-Lerida I, Lazcano JJ, Samaniego R, Calvo E, Tello M, Osteso-Ibanez T, Pellinen T, Echarri A, Cerezo A, Klein-Szanto AJ, Garcia R, Keely PJ, Sanchez-Mateos P, Cukierman E, Del Pozo MA. Cell. 2011;146:148–163. doi: 10.1016/j.cell.2011.05.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhang K, Corsa CA, Ponik SM, Prior JL, Piwnica-Worms D, Eliceiri KW, Keely PJ, Longmore GD. Nature cell biology. 2013;15:677–687. doi: 10.1038/ncb2743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lyons TR, O'Brien J, Borges VF, Conklin MW, Keely PJ, Eliceiri KW, Marusyk A, Tan AC, Schedin P. Nature medicine. 2011;17:1109–1115. doi: 10.1038/nm.2416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Provenzano PP, Inman DR, Eliceiri KW, Knittel JG, Yan L, Rueden CT, White JG, Keely PJ. BMC Med. 2008;6:11. doi: 10.1186/1741-7015-6-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nam KH, Kim P, Wood DK, Kwon S, Provenzano PP, Kim DH. Scientific reports. 2016;6:29749. doi: 10.1038/srep29749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Roy R, Boskey A, Bonassar LJ. J Biomed Mater Res A. 2010;93:843–851. doi: 10.1002/jbm.a.32231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mason BN, Reinhart-King CA. Organogenesis. 2013;9:70–75. doi: 10.4161/org.24942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Truong D, Puleo J, Llave A, Mouneimne G, Kamm RD, Nikkhah M. Sci Rep. 2016;6:34094. doi: 10.1038/srep34094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Blacher S, Erpicum C, Lenoir B, Paupert J, Moraes G, Ormenese S, Bullinger E, Noel A. PLoS One. 2014;9:e97019. doi: 10.1371/journal.pone.0097019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kato M, Suzuki T, Suzuki Y, Terasawa Y, Sasano H, Arai Y. J Urol. 2004;172:863–866. doi: 10.1097/01.ju.0000136315.80057.99. [DOI] [PubMed] [Google Scholar]
- 44.Mandonnet E, Delattre JY, Tanguy ML, Swanson KR, Carpentier AF, Duffau H, Cornu P, Van Effenterre R, Alvord EC, Capelle L. Ann Neurol. 2003;53:524–528. doi: 10.1002/ana.10528. [DOI] [PubMed] [Google Scholar]
- 45.Provenzano PP, Inman DR, Eliceiri KW, Beggs HE, Keely PJ. Am J Pathol. 2008;173:1551–1565. doi: 10.2353/ajpath.2008.080308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Carlson M, Watson AL, Anderson L, Largaespada DA, Provenzano PP. J Biomed Opt. 2017;22:1–9. doi: 10.1117/1.JBO.22.11.116010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Carpenter AE, Jones TR, Lamprecht MR, Clarke C, Kang IH, Friman O, Guertin DA, Chang JH, Lindquist RA, Moffat J, Golland P, Sabatini DM. Genome Biol. 2006;7:R100. doi: 10.1186/gb-2006-7-10-r100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Thévenaz P, Ruttimann UE, Unser M. IEEE Trans Image Process. 1998;7:27–41. doi: 10.1109/83.650848. [DOI] [PubMed] [Google Scholar]
- 49.Dickinson RB, Tranquillo RT. Journal. 1993;39:1995–2010. [Google Scholar]
- 50.Castle B, Odde D. Biophysical Journal. 2013;105:2528–2540. doi: 10.1016/j.bpj.2013.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ermak D, McCammon J. Journal of Chemical Physics. 1978;69:1352–1360. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.