Abstract
Temporal changes to the concentration of molecular species such as mRNA, which take place in response to various environmental cues, can often be modeled as simple continuous functions such as a single pulse (impulse) model. The simplicity of such functional representations can provide an improved performance on fundamental tasks such as noise reduction, imputation and differential expression analysis. However, temporal gene expression profiles are often studied with models that treat time as a categorical variable, neglecting the dependence between time points. Here, we present ImpulseDE2, a framework for differential expression analysis that combines the power of the impulse model as a continuous representation of temporal responses along with a noise model tailored specifically to sequencing data. We compare the simple categorical models to ImpulseDE2 and to other continuous models based on natural cubic splines and demonstrate the utility of the continuous approach for studying differential expression in time course sequencing experiments. A unique feature of ImpulseDE2 is the ability to distinguish permanently from transiently up- or down-regulated genes. Using an in vitro differentiation dataset, we demonstrate that this gene classification scheme can be used to highlight distinct transcriptional programs that are associated with different phases of the differentiation process.
INTRODUCTION
Time course sequencing experiments such as RNA-seq, ChIP-seq and ATAC-seq yield a description of the development of a cellular system over time. Such a dynamic description can be used to analyze the timing of cellular programs and can uncover transitional responses that are not observed if only initial and terminal cell states are compared. These dynamic properties give insights into the regulatory molecular circuits that drive the developmental process.
Differential expression analysis is frequently used to reduce time course (longitudinal) datasets to genes with varying expression profiles across conditions to ease downstream analytic tasks. Differential expression analysis algorithms for time course datasets can be divided into methods that treat time points independently and methods that explicitly model the dependence between time points. Methods that utilize the former approach are mostly based on generalized linear models, with the sampling time point as a categorical variable that is then used as a predictor for the expression level. These models are implemented in the context of popular software packages such as DESeq (1), DESeq2 (2), edgeR (3) and limma (4). Methods that utilize the latter approach constrain the sequence of measured expression levels to a continuous function of time, thus capturing the dependence of expression levels between time points. Such continuous dependence on time has previously been captured with linear models based on a spline basis transform of the time coordinate (edge (5) and limma (4)) or with non-linear models (impulse model in ImpulseDE (6)). Notably, while any differential expression framework based on a generalized linear model can in principle be used with a natural cubic spline basis to produce continuous fits, in many cases (e.g. DESeq2) such extensions have rarely been discussed to date.
Importantly, categorical time models suffer from a relative loss of statistical testing power, especially if many time points are observed, relative to continuous models, which have a fixed number of parameters. Furthermore, categorical time models are difficult to use if expression trajectories are compared between conditions that were sampled at different time points (as may be the case if samples are taken from human donors). Conversely, continuous expression models of time can address this shortcoming by comparing fitted values in unmeasured time points implicitly.
Here, we present ImpulseDE2, a differential expression algorithm for longitudinal sequencing experiments. Like its predecessor, ImpulseDE, ImpulseDE2 models the gene-wise expression trajectories over time with a descriptive single-pulse (impulse) function (Figure 1) (7,8). However, unlike ImpulseDE, which uses an empirical null model based on randomization of the original data, ImpulseDE2 employs a noise model specific to count data from multiple batches and combines it with a likelihood ratio test, leading to much faster and more accurate inference (Supplementary Figure S1). Notably, ImpulseDE2 was favorably mentioned in a recent benchmarking study on differential gene expression in time course datasets (9).
Figure 1.
The impulse model is descriptive of global transcriptome and chromatin dynamics during the cellular response to stimuli. (A) The four classes of expression trajectories that can be modeled with the impulse model. (B) Case-only analysis: shown are an impulse fit (alternative model) and a constant fit (null model) with vertically superimposed inferred negative binomial likelihood functions. The likelihood functions are scaled and shifted so that the density is zero at the time coordinate of the time point of sampling. (C) Case–control analysis: shown are a separate case and control impulse fit (alternative model) and a single impulse fit to all samples (‘combined’, null model). (D–H) Heat maps of z-scores of library depth normalized mean counts per time point of differentially expressed genes selected with DESeq2. Green stars indicate clusters that can be modeled with the valley model. (D) RNA-seq of Drosophila melanogoster development (‘Drosophila (Graveley)’ dataset (17)). (E) Chromatin immunoprecipitation (ChIP) of the H3K4me1 histone mark in the erythroid lineage in hematopoesis (‘erythroid chromatin (Lara-Astiaso)’ dataset (14)). The x-coordinates are seven cell states in developmental order (‘developmental times’ one to seven) within the erythroid lineage. (F) RNA-seq of dendritic cell activation through LPS (‘LPS (Jovanovic)’ dataset (15)). (G) RNA-seq of myeloid differentiation (‘myeloid (Sykes)’ dataset (18)). (H) RNA-seq of differentiation of human embryonal stem cells to definite endoderm (‘hESC (Chu)’ dataset (19)). Heat map of two further datasets (‘estrogen (Baran-Gale)’ (16) and ‘Plasmodium (Broadbent)’ dataset (20)) are supplied in Supplementary Figure S2.
In the following, we use four different datasets to demonstrate that ImpulseDE2 outperforms ImpulseDE, as well as the categorical model of DESeq2 (with standard settings), and the continuous temporal models implemented with edge and limma. We then propose ways to extend these existing methods to improve their performance on time course data. To this end, we discuss the purpose and consequences of low mean expression gene filtering for limma and edge. We further show how one can improve the performance of DESeq2 by using a natural cubic spline basis (referred to as DESeq2splines) instead of a categorical representation of time, non-standard batch correction in case–control analysis and high-dispersion outlier handling. Through this analysis, we propose settings for DESeq2 (e.g. using splines) that are best suited for time course studies and demonstrate how out-of-the-box ImpulseDE2 can perform better or similarly well across all performance indicators and datasets.
At last, we introduce a hypothesis testing scheme that can be used to identify transiently and permanently activated or deactivated genes. These classes of transient and permanent changes directly relate to the biological process of cell activation or differentiation: over the course of the response of a cell to a stimulus, the cell moves from one state in the transcriptome space to another state. ImpulseDE2 can distinguish genes responsible for the differences between the states (permanent changes) and genes that change transiently during the transition between the cell states.
MATERIALS AND METHODS
ImpulseDE2 fits an impulse model (7,8) (Equation 1) to time course count data and performs differential expression analysis based on the model fits with a log-likelihood ratio test. The central covariate considered in ImpulseDE2 is continuous time. Furthermore, if trajectories from two different conditions (case and control) are compared, a discrete condition indicator covariate is added. At last, if batch structure is present in the data beyond the case and control conditions, a categorical batch assignment covariate is added for each confounding variable.
We distinguish case-only and case–control differential expression analysis. Case-only differential expression analysis looks for genes with changing expression over time. In this analysis, an impulse fit to the expression values over time is compared to a constant fit. In the second mode, namely case–control differential expression analysis, we are looking for genes with expression profiles that differ between two time courses (representing two conditions). In this analysis, the alternative model is represented by separate impulse model fits to each condition, while the null model is represented by a single impulse model fit to both conditions. ImpulseDE2 can additionally correct for batch effects through a gene and batch specific factor in the gene expression model. Multiple confounding variables with differing batch structures can be modeled if the corresponding design matrix is full rank.
The impulse model
ImpulseDE2 models the expression level of a gene as a function of time with the function fImpulse. The impulse function is the scaled product of two sigmoid functions (Equation 1) (7) and has three state-specific expression values: initial, peak and steady state. The two sigmoid functions represent the transitions of initial state to peak state and peak state to steady state.
 |
(1) |
where the amplitude parameters are h0 = fImpulse(t → −∞), h2 = fImpulse(t → ∞) (steady state expression) and h1 models the intermediate expression, t1 and t2 are the state transition times, β is the slope parameter of both sigmoid functions. One could use two different slope parameters but we use a shared slope parameter to reduce the number of parameters of the model.
The likelihood function
We assume that the number of reads x generated from μ transcripts is negative binomially distributed. The likelihood  of the count data xi, . of gene i observed in J samples at time points tj is:
of the count data xi, . of gene i observed in J samples at time points tj is:
 |
(2) |
where  is the negative binomial likelihood:
is the negative binomial likelihood:
 |
(3) |
The mean expression at each time point μi(tj) is determined by a fit of the impulse model fImpulse(t) (Equation 1) to the time course data. Similarly, the underlying impulse model trend is replaced by a sigmoid or by a constant model as required for the hypothesis tests presented below. Other parameters of the model are: a sample-specific size factor 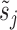 , which corrects for library size and gene-specific batch correction factors Ci (in log space), which correspond to a model matrix X that encodes batch assignments or other sample-specific covariates. One can incorporate guanine-cytosine content bias correction via sample-specific normalization constants or by supplying normalized count data (10). One has to take care that the negative binomial distribution assumption is not violated if normalized data are supplied (10). At last, the dispersion factor
, which corrects for library size and gene-specific batch correction factors Ci (in log space), which correspond to a model matrix X that encodes batch assignments or other sample-specific covariates. One can incorporate guanine-cytosine content bias correction via sample-specific normalization constants or by supplying normalized count data (10). One has to take care that the negative binomial distribution assumption is not violated if normalized data are supplied (10). At last, the dispersion factor 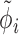 links the mean of the negative binomial distribution to its variance (Equation 4).
links the mean of the negative binomial distribution to its variance (Equation 4).  is pre-estimated as a constant hyperparameter for each gene with DESeq2 (2).
is pre-estimated as a constant hyperparameter for each gene with DESeq2 (2).
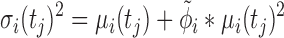 |
(4) |
Parameter estimation and differential expression analysis
The overall likelihood of the data is the product of the gene-wise likelihoods. Therefore, the optimization of the model parameters based on the likelihood intuitively lends itself to parallelization over genes. We performed gene-wise impulse model parameter estimation with the Broyden–Fletcher–Goldfarb–Shanno algorithm (Supplementary Notes Section S2). The set of parameters estimated for the impulse model is {h0, h1, h2, t1, t2, β}, which does not contain the constant hyperparameters 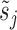 and
and  .
. 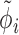 is estimated with DESeq2 and treated as a constant during impulse model fitting.
is estimated with DESeq2 and treated as a constant during impulse model fitting.
We perform differential expression analysis using a log-likelihood ratio tests by comparing the likelihood of the null with the alternative model using the χ2-distributed deviance test statistic (Supplementary Notes Sections S1 and S2.3).
Reference methods
We used ImpulseDE2, DESeq2 and DESeq2splines on rounded expected count matrices (Supplementary Notes Section S5). We used DESeq2 in the log-likelihood ratio test mode in all cases. We used ImpulseDE, edge and limma on scaled data, where the scaling factor is determined as the DESeq2 size factor (2). Therefore, the same library size normalization was used for ImpulseDE2, DESeq2, ImpulseDE, edge and limma. Before using edge and ImpulseDE, we log transformed the normalized expected counts (log(x + 1)). We used voom (11) to transform the data before fitting the linear model with limma. We used DESeq2splines, limma and edge with a natural cubic spline basis with four degrees of freedom. All analysis performed is based on P-values and Benjamini–Hochberg (12) corrected P-values. We did not use method specific false-discovery rate (FDR) adjustment algorithms to make the results comparable.
Overview datasets
Table 1 summarizes all datasets presented in this study. The datasets Plasmodium (Broadbent) and estrogen (Baran-Gale) were only used to show heat maps in Supplementary Figure S2 to highlight the occurrence of expression patterns with the impulse model shape in these scenarios. UpSetR plots are supplied for the analysis of all other datasets in Supplementary Figures S10–S14. In the iChIP (Jovanovic) dataset, genes were replaced with iChIP peaks called with MACS2 (13) and the signal is the number of reads overlapping a peak.
Table 1.
Datasets presented in this study
| Dataset | Time points | Batches | Controls | Heat map | Analysis | Reference |
|---|---|---|---|---|---|---|
| LPS (Jovanovic) | 7 | 2 | case–control | Figure 1 | Figure 3, Supplementary Figures S3 and S4 | (15) |
| Drosophila (Graveley) | 23 | 2–3 | case-only | Figure 1 | Supplementary Figure S5 | (17) |
| Myeloid (Sykes) | 10 | 2 | case-only | Figure 1 | Figure 4, Supplementary Figures S6 and S7 | (18) |
| hESC (Chu) | 6 | 3 | case-only | Figure 1 | Figure 5Supplementary Figure S8 | (19) |
| iChIP (Jovanovic) | 7 | 1 | case-only | Figure 1 | Supplementary Figure S9 | (14) |
| Plasmodium (Broadbent) | 10 | 1 | case-only | Supplementary Figure S2 | – | (20) |
| Estrogen (Baran-Gale) | 10 | 1 | case-only | Supplementary Figure S2 | – | (16) |
RESULTS
ImpulseDE2 is a differential expression algorithm that combines a parametric model for the expression trajectory across time (impulse model, Figure 1A) with a negative binomial noise model (Figure 1B). ImpulseDE2 has two modes of operation: single-condition differential expression analysis (‘case-only’) and two-condition differential expression analysis (‘case–control’). Case-only differential expression analysis identifies genes that have non-constant expression trajectories over time from samples of a single condition (Figure 1B). Case–control differential expression analysis identifies genes that have different expression trajectories over time between two conditions (such as with and without a stimulus or treatment at time point zero) (Figure 1C).
We compared ImpulseDE2 with the following reference methods: DESeq2 that is based on a categorical time expression model and that has a negative binomial noise model, DESeq2 with a natural cubic spline basis transform of the time coordinate (below referred to as DESeq2splines), edge that is based on natural cubic splines as expression model with a non-parametric noise model in log space, limma that is based on natural cubic splines as expression model with a Gaussian noise model in log space and ImpulseDE that is based on the impulse model as the expression model with a non-parametric noise model.
The impulse model is descriptive of global transcriptome and chromatin dynamics during the cellular response to stimuli
We considered a comprehensive collection of sequencing-based temporal datasets, covering several organisms, molecular species, biological processes and time scales. Specifically, the presented datasets include histone mark dynamics during development (14) (Figure 1E), expression profiles of cell cultures in response to environmental stimuli (15,16) (Figure 1F and Supplementary Figure S2) and expression profiles of cell cultures in response to developmental stimuli (17–20) (Figure 1D, G and H; Supplementary Figure S2).
We selected differentially expressed genes without explicitly constraining to a single-pulse behavior, by using DESeq2 with a categorical model of time. We then clustered the expression profiles of the selected genes over time (Figure 1D–H and Supplementary Figure S2). Evidently, most of the selected molecular species can be modeled with the impulse model with a single ‘peak’ or ‘valley’. There are a few exceptions that have a weak bimodal behavior, which can also be approximated with a unimodal model. For instance, considering the Drosophila melanogaster development data (Figure 1D), we note that most genes peak only once over an entire developmental time course from an embryo to an adult organism. Note that in many experimental settings, one would only be interested in a subprocess of the entire development, such as one of the embryo stages: larvae, pupae or adult. The single-peak or -valley assumption agrees well with the data in these subprocesses.
Fundamental limits of categorical frameworks on longitudinal data
Continuous models, such as linear models based on a natural cubic spline basis transform or non-linear parametric models can be used with a fixed number of degrees of freedom irrespective of the number of time points sampled, whereas categorical models require one degree of freedom per sampled time point. In case-only differential expression analysis, the null model is usually a constant model and its number of degrees of freedom therefore is independent of the number of time points. Accordingly, the difference in degrees of freedom of the full (alternative) and the reduced (null) models in the differential expression test is constant for continuous models and grows linearly for categorical models. Therefore, the relative statistical power of a continuous framework increases compared to a categorical framework with the number of time points samples.
We showed this difference in statistical power in simulations with varying number of time points and a mix of generative models in a case-only scenario (see Supplementary Methods Section S7 for description of the simulation process). Each simulated dataset consists of 1500 differentially expressed (DE) genes and 1000 non-DE genes. The non-DE genes are simulated as noisy samples from a constant expression level over time, while the DE genes are noisy samples taken from either a linear, sigmoidal or impulse-like function of time (500 genes each). We sampled three independent and identically distributed replicates per time point based on negative binomial noise and assessed the statistical testing power of each method as the area under the receiver-operator characteristic curve (AUROC) of the differential expression cells. Here, the binary classifier is significance of differential expression and the variable threshold parameter is the significance threshold for the Benjamini–Hochberg corrected P-values.
Considering the resulting AUROC values, it is clear that most continuous frameworks (namely, ImpulseDE2, DESeq2splines, edge and limma) outperform the categorical framework DESeq2 and that ImpulseDE2 outperforms ImpulseDE (Figure 2A). Limma based on a spline model with very few (two) degrees of freedom performs very well in this comparison as we used simple functional forms for the simulated trajectories. Models with few degrees of freedom may miss transient patterns on real data so that we do not recommend using such models on real data.
Figure 2.
ImpulseDE2 performance on simulated data (ROC and FDR data). AUC: area under the curve, df: degrees of freedom, FDR: false-discovery rate, ROC: receiver-operator characteristic. (A) AUC of ROC curve for case-only differential expression analysis with a varying number of time points (5–12 time points with three replicates each). (B) FDR for case-only analysis based on random deviation of a constant trend. The strength of the random variation is quantified by the standard deviation of the normal distribution from which the deviation from the constant trend is drawn for each sample. ImpulseDE was not included in this simulation study due to its slow run time and as this panel was included to compare the discovery rates of categorical and continuous models on random trends.
Condition-wise batch correction outperforms global batch correction
It is difficult to benchmark differential expression frameworks because there is typically no ground truth other than in simulation scenarios. To address this, we propose a metric to evaluate differential expression results based on annotated gene sets: the gene responsiveness score. The responsiveness of a gene is defined as the number of published studies (from a pool of available studies) that annotated that gene as differentially expressed under settings related to the ones under investigation. For instance, in the context of the LPS (Jovanovic) dataset (15) (Figure 1F), the responsiveness score of a gene will reflect the number of published datasets (RNA-seq or microarrays) of dendritic cell stimulation through toll-like receptor 4 or other toll-like receptors in which this gene was reported as differentially expressed.
Our assumption in using this score is that the more annotated gene sets related to the target process contain a gene, the more confident we can be that this gene should be called as differentially expressed. Based on this assumption, one can then compare two algorithms for differential expression at a given significance threshold based on the number of called genes as well as the distribution of their responsiveness scores. Specifically, a non-empty set of genes that were called by only one method reflects an advantage in type II error rate (false negatives) or a disadvantage in type I error rate (false positives). The responsiveness of the genes in this set can then be used to evaluate the relative contribution of true positive and false positives to this set.
A good resource that includes a large pool of such differential expression annotations in the context of immune cells is the ImmuneSigDB (21) collection. We used this resource to evaluate the performance of the different algorithms on the LPS (Jovanovic) dataset, a well studied system with a large set of relevant published transcriptional datasets. The LPS (Jovanovic) dataset consists of samples of seven time points in two conditions (with and without lipopolysaccharide (LPS) addition at time point 0 h). To compute the responsiveness scores in this context, we computed for each gene the number of ImmuneSigDB (21) transcriptional genes sets that contain ‘dendritic cell’ (DC) and ‘lipopolysaccharide’ (LPS) or ‘toll-like receptor’ (TLR) in their description. We used these scores for pairwise comparison between methods, where we analyzed the overall responsiveness of the sets of genes that are only called by one method and not the other. Specifically, we compared ImpulseDE2 to DESeq2, DESeq2splines, limma and edge based on the mutually exclusive differential expression cells at a Benjamini–Hochberg corrected P-value of 0.01 both for case-only and case–control analysis.
We found that in both case-only and case–control setting, ImpulseDE2 reports substantially more genes than DESeq2 (Figure 3A and E) and edge (Figure 3D and H). Furthermore, we find that genes reported only by ImpulseDE2 are similarly or more responsive than genes uniquely called by each of these two methods, indicating that the higher number of DE genes may reflect a decrease in type II error rather than an increase in type I error. Limma reports more DE genes than ImpulseDE2 in both scenarios (Figure 3C and G). However, those DE genes only called by limma are less responsive than the DE genes only called by ImpulseDE2, which suggests that limma has a higher type I error rate than ImpulseDE2 (Figure 3C and G). Comparing to DESeq2splines, we find that, in the case-only settings, ImpulseDE2 reports less genes; however, the genes uniquely reported by ImpulseDE2 are more responsive than the ones reported only by DESeq2splines (Figure 3B). In the case–control setting, ImpulseDE2 reports less genes, while the distributions of responsiveness scores of the genes identified exclusively by each method are similar.
Figure 3.
Overlaps to annotated gene sets indicate that ImpulseDE2 identifies more relevant genes than DESeq2, edge and limma on LPS (Jovanovic) dataset. Background: all genes analyzed. ImpulseDE2: genes only called differentially expressed by ImpulseDE2 and not by the reference method at a Benjamini–Hochberg corrected P-value threshold of 0.01. DESeq2 (A and E), DESeq2splines (B and F), limma (C and G), edge (D and H): genes only called differentially expressed by the reference method and not ImpulseDE2 at a Benjamini–Hochberg corrected P-value threshold of 0.01. n: gene set size. ECDF: empirical cumulative density function, KS: log10 P-value of one sided Kolmogorov–Smirnov test for the ECDFs of the set of the given method to lie below the ECDF of the other method considered in the plot. The ECDF are based on the number of overlapping ImmuneSigDB (21) target sets with each gene in the individual gene sets: the target set was all ImmuneSigDB sets that contain any the following strings in their names: ‘‘DC’’, ‘‘DENDRITIC’’ (empty, all listed under DC), ‘‘LPS’’ or ‘‘TLR’’. (A–D) Case-only differential expression analysis. (E–H) Case–control differential expression analysis.
The LPS dataset (both case and control conditions) was sampled twice, yielding two batches. The correlation matrix of all samples suggests that there are strong batch effects in this dataset (Supplementary Figure S3). Frameworks for differential expression analysis based on generalized linear models allow for batch effect correction during model fitting through coefficients for batch identity covariates in the linear model (2). ImpulseDE2 performs batch correction separately within each condition (case and control) in the full model as the case and control profiles are fit separately. The differences between ImpulseDE2 and the DESeq2-based approaches (DESeq2 and DESeq2splines) in the case–control analysis (Supplementary Figure S4a,b and d) may be attributed to the differences in the way batches are handled. To explore this, we introduced the condition-wise batch correction in the DESeq2-based models to test whether the differences in model performance are due to the batch model. Indeed, we found that the categorical model DESeq2 with condition-wise batch correction yields very similar P-values for differential expression to ImpulseDE2 (Supplementary Figure S4a,c).
In summary, the gene set annotation based analysis suggests that ImpulseDE2 outperforms edge, limma and DESeq2. We also find that one can improve the performance of the latter by using condition-wise batch correction. Compared with DESeq2splines, we find that ImpulseDE2 reports less genes, albeit with similar or higher responsiveness scores. We note that this difference in detection rate between ImpulseDE2 and DESeq2splines is not a general property, as we have observed little difference (Figure 4A; Supplementary Figures S8a and S9a) or even an opposite trend (Supplementary Figure S5a) in other datasets.
Figure 4.
Comparison of ImpulseDE2, DESeq2, limma and edge on myeloid (Sykes) dataset. (A) Fraction of significantly differentially expressed genes as a function of the significance threshold by method. (B–E) Correlation plot of the inferred differential expression Benjamini–Hochberg (BH) corrected P-values for all genes between ImpulseDE2 and DESeq2 (B), DESeq2splines (C), edge (D) and limma (E). Orange points correspond to genes for which ImpulseDE2 disabled DESeq2 dispersion outlier handling. (F) Kernel density estimate of density of the distribution of expression means of genes called differentially expressed at a q-value threshold of 1e − 2 of ImpulseDE2, limma and edge. The mean expression distribution across all genes is shown as all genes. The UpSetR plot for this dataset is supplied in Supplementary Figure S10.
DESeq2 with standard settings misses differentially expressed genes that contain zero count observations
Globally, ImpulseDE2 and DESeq2 give similar results on the myeloid (Sykes) dataset (Figure 4A and B). We observed that there are 72 genes that are detected by ImpulseDE2 and not by DESeq2 (Figure 4B and Supplementary Figure S5b) that are enriched in gene ontology (GO) biological process (22) gene sets related to the immune system (Supplementary Data S1) and that contain observations with zero counts. These 72 genes are labeled as high variance outliers by DESeq2 and are therefore not regularized in the empirical Bayes dispersion estimation step of DESeq2. To address this, we implemented a correction step in ImpulseDE2, which automatically identifies genes with overestimated variances and corrects the dispersion estimates to the maximum a posteriori estimates from DESeq2 (‘Materials and Methods’ section). Because of the lower variance estimate, ImpulseDE2 can identify these genes as differentially expressed while they are missed by DESeq2 (Figure 4B, also observed on another dataset in Supplementary Figure S5b). These genes that were labeled as dispersion outliers by DESeq2 contain very clear cases of differential expression (Supplementary Figure S6). One can detect these variance outlier genes with DESeq2 without strong effects on the global results if the dispersion outlier calling is altered in DESeq2 as described in the Supplementary Methods Section S6.2. The dispersion outlier standard settings of DESeq2 are conservative so that the variance is not underestimated. We showed that this may yield undesirable results on genes with zero count observations.
DESeq2 detects multimodal expression profiles as differentially expressed
There are also genes which receive lower P-values by DESeq2 (bottom right half of Figure 4B). We visually observed that these genes have mostly multimodal temporal profiles (Supplementary Figure S7). Continuous expression models tailored to unimodal expression profiles (the impulse model and natural cubic splines with few degrees of freedom) under-fit such multimodal trajectories and therefore fit part of the variation as noise. Accordingly, frameworks based on such continuous models assign lower P-values for differential expression to such multimodal trajectories (Figure 2B). An analyst has to decide for each project whether such multimodal trajectories are of interest. It is important to keep in mind that such trajectories can be explained by noise if few replicates are sampled or batch correction is difficult.
ImpulseDE2 and DESeq2 outperform limma on genes with low average expression
We observed large differences in the global differential expression results of ImpulseDE2 and limma on the myeloid (Sykes) dataset (Figure 4A and E). Many of the genes only labeled differentially expressed by edge or limma and not by ImpulseDE2 have low average expression (Figure 4F), which we also observed on the hESC (Chu) data (Supplementary Figure S8f) and the Drosophila (Graveley) data (Supplementary Figure S5f). Indeed, the authors of voom employ filtering of genes with low mean expression before running limma–voom (11). This is sensible in terms of the framework of limma–voom: a normal distribution in log-space that does not account for the largely discrete nature of count data in the low expression range. ImpulseDE2 and DESeq2 account for the count data type through their negative binomial noise model. However, we argue that filtering genes with low expression before differential expression analysis is not a desirable solution: Firstly, one may be interested in those genes with low mean expression. Secondly, any filtering step is highly dataset dependent and will therefore often lead to situations in which genes are missed because of suboptimal filtering. Given a time course with 10 sampled time points, a gene with zero expression throughout which increases to a transcript count of 19 at the last time point would be excluded by a very lenient minimum mean expression filter of two already. The omission of such an expression profile is undesirable if this was observed across replicates. There are 115 genes in the myeloid (Sykes) dataset with average expression below two, which were called differentially expressed by DESeq2splines at a significance threshold on the false-discovery corrected P-value of 0.01 and 567 genes with average expression below five, these genes are potentially false negatives in the limma-based analysis.
We therefore argue that such gene filtering has the potential to introduce false negative differential expression calls. The inclusion of genes with low average expression in the limma–voom pipeline results in a large number of differential expression cells of these genes with low average expression (Figure 4F), which may include false positives as the limma–voom noise model is not appropriate for these genes.
ImpulseDE2 identifies genes with transiently changing expression level
The response of a cell to a stimulus can often be viewed as a transition of the population from one transcriptomic state to another transcriptomic state, such as in cell activation or differentiation (8). A biologically more interesting question than simple differential expression may be whether a gene is induced transiently (which may indicate involvement in transitional phases) or more permanently (indicative of potential importance in the terminal phenotype) (23).
We introduce a hypothesis testing scheme that is able to answer these questions. To this end, we use a third model—a monotonous sigmoid that is indicative of maintained modulation of expression (up- or down- regulation). We compare the fit to this model to an impulse model and a constant model. We define transiently regulated genes as genes, which are significantly better fit by an impulse model than by a sigmoid model and which do not have a monotonous impulse model fit (Supplementary Methods Section S2.3). We define permanently regulated genes as genes that are not transient but that are significantly better fit by a sigmoid than by a constant model. We classify up- and down-regulated genes in the transient and the permanent class based on their impulse model fits.
We analyzed the performance of the expression profile stratification by ImpulseDE2 on a six time point RNA-seq dataset of in vitro human embryonic stem cell differentiation (19). The heat map of expression profiles sorted by their peak times within each class shows that ImpulseDE2 can indeed classify expression trajectories into transiently and permanently changing trajectories (Figure 5).
Figure 5.
ImpulseDE2 can distinguish between transiently and permanently changing expression trajectories in hESC (Chu) dataset. Shown are z-scores of size-factor normalized mean expression values per time point. Selected top enrichments with GO biological process, GO molecular function and MSigDB hallmark gene sets are supplied to the right of each group.
We find a large group of genes that is transiently down-regulated from 0 to 72 h after differentiation induction. The top gene set enrichment hit of the transiently down-regulated genes against the GO molecular function gene sets (22) is oxidoreductase_activity and the top enrichment with respect to the MSigDB hallmark set is oxidative phosphorylation (Supplementary Data S2). It was shown that human embryonic stem cells can be induced to differentiate by hypoxic conditions (19). We argue that the observed down-regulation of genes related to oxidative phosphorylation during differentiation may provide a mechanistic link to the differentiation induction by hypoxia: down-regulation of oxidative phosphorylation related processes is a molecular (e.g. transcriptomic or metabolic) signature that is induced by and drives differentiation. Therefore, differentiation can be directly induced by inducing this signature through hypoxia. We note that the optimal hypoxia treatment for differentiation induction coincides with the time frame of down-regulation of the oxidative phosphorylation related gene set (0–72 h (19) and Figure 5).
Moreover, we find a succession of transiently up-regulated genes that would be expected as result of a signaling cascade that drives the transition from initial state to final state (reached at 72 h). Indeed, the top gene set enrichment hits of these transiently up-regulated genes against the GO molecular function gene sets contain many nucleic acid binding terms, suggesting gene expression regulation cascades are active.
The top three enrichments of permanently down-regulated genes against the MSigDB hallmark gene sets (24) contain two Myc-target sets which suggest that this gene set represents the loss of embryonic cell identity. The top enrichments of permanently up-regulated genes against the GO biological process gene sets (22) contain several tissue development terms which suggest that this gene set represents the gain in differentiated cell identity.
In summary, we find that genes with transient expression trajectories reflect transient processes in the population and genes with monotonous expression trajectories reflect differences in the cell states (embryonic and definite endoderm).
DISCUSSION
We motivated the use of the impulse model by showing that transcriptomic and epigenomic dynamics of cells in response to environmental and developmental stimuli can often be modeled with a single maximum or a minimum per gene. We note that similar functional forms can be achieved with natural cubic splines models with few degrees of freedom (such as three or four degrees of freedom). The impulse model has previously been used in the differential expression tool ImpulseDE. ImpulseDE is based on a non-parametric noise model. Here we introduce ImpulseDE2, a differential expression algorithm, which is based on the impulse model and which is tailored to count data. The altered noise model makes ImpulseDE2 50 times faster than ImpulseDE (Supplementary Figure S8) and yields better differential expression results on count data, such as produced by RNA-seq, ChIP-seq (Supplementary Figure S9) and ATAC-seq.
We showed that continuous expression models outperform categorical models if more time points than degrees of freedom of the continuous model are sampled. We introduced the gene responsiveness metric and gene set enrichment analysis of sets of mutually exclusive differential expression cells to benchmark differential expression methods. ImpulseDE2 works well out-of-the-box compared to all other methods across datasets. We described how DESeq2 can be brought to similar performance with non-standard settings. On the other hand, limma and edge have disadvantages on genes with low expression mean and we discussed why gene filtering is not always desirable. We therefore suggest the use of ImpulseDE2 or DESeq2 with the settings described here for time course differential expression analysis. One can base this decision on the continuous model used: ImpulseDE2 has a rigid expression model that is unlikely to overfit random fluctuations in very noisy data, DESeq2 based on splines can be used to extract expression profiles of all shapes, depending on the number of degrees of freedom used. It makes sense to use continuous models in time if at least as many time points as the number of degrees of freedom used were sampled: six or more time points for ImpulseDE2, n or more time points if a spline model with n degrees of freedom is used for DESeq2, limma or edge.
ImpulseDE2 relies on estimation of a non-linear model for expression as a function of time. Disadvantages of such models include numerical estimation problems and local maxima of the log-likelihood cost function. We guarded against both problems in the implementation through multiple initializations and through numerical thresholds. ImpulseDE2 did not produce numerical errors on any analyzed dataset.
At last, we combine impulse model fits with constant and sigmoid model fit to identify genes with transiently or monotonously changing trajectories and show that these automatically annotated gene sets represent biologically meaningful groups of genes. Our analysis suggests a mechanism for hypoxia-induced human embryonic stem cell differentiation.
DATA AVAILABILITY
ImpulseDE2 is available through Bioconductor and through Github (https://github.com/YosefLab/ImpulseDE2). We made instructions for the usage of DESeq2 with a natural cubic spline basis for temporal data available as Supplementary Data S3.
Supplementary Material
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
German Research Foundation (DFG) Fellowship, Graduate School of Quantitative Biosciences Munich (QBM) [GSC 1006 to D.S.F.]; BaCaTeC; Joachim Herz Stiftung (to D.S.F.). Funding for open access charge: Federal funds.
Conflict of interest statement. None declared.
REFERENCES
- 1. Anders S., Huber W., Anders S., Huber W.. Differential expression analysis for sequence count data. Genome Biol. 2010; 11:R106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Michael I.L., Huber W., Anders S.. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014; 15:550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Mark D., Robinson D.J., McCarthy Smyth G.K.. edgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2009; 26:139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Matthew E., Ritchie B.P., Wu D., Hu Y., Law C.W., Shi W., Smyth G.K.. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015; 43:e47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Storey J.D., Xiao W., Leek J.T., Tompkins R.G., Davis R.W.. Significance analysis of time course microarray experiments. Proc. Natl. Acad. Sci. U.S.A. 2005; 102:12837–12842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Sander J., Schultze J.L., Yosef N.. ImpulseDE: detection of differentially expressed genes in time series data using impulse models. Bioinformatics. 2016; 33:757–759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Chechik G., Koller D.. Timing of gene expression responses to environmental changes. J. Comput. Biol. 2009; 16:279–290. [DOI] [PubMed] [Google Scholar]
- 8. Yosef N., Regev A.. Impulse control: temporal dynamics in gene transcription. Cell. 2011; 144:886–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Spies D., Renz P.F., Beyer T.A., Ciaudo C.. Comparative analysis of differential gene expression tools for RNA sequencing time course data. Brief. Bioinform. 2017; doi:10.1093/bib/bbx115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Risso D., Schwartz K., Sherlock G., Dudoit S.. GC-Content normalization for RNA-Seq Data. BMC Bioinform. 2011; 12:480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Law C.W., Chen Y., Shi W., Smyth G.K.. Voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol. 2014; 15:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Benjamini Y., Hochberg Y.. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B. 1995; 57:289–300. [Google Scholar]
- 13. Feng J., Liu T., Qin B., Zhang Y., Liu X.S.. Identifying ChIP-seq enrichment using MACS. Nat. Protoc. 2012; 7:1728–1740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Lara-Astiaso D., Weiner A., Lorenzo-Vivas E., Zaretsky I., Jaitin D.A., David E., Keren-Shaul H., Mildner A., Winter D., Jung S.. Chromatin state dynamics during blood formation. Science. 2014; 345:943–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Jovanovic M., Rooney M.S., Mertins P., Przybylski D., Chevrier N., Satija R., Rodriguez E.H., Fields A.P., Schwartz S., Raychowdhury R. et al. Immunogenetics. Dynamic profiling of the protein life cycle in response to pathogens. Science. 2015; 347:1259038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Baran-gale J., Purvis J.E., Sethupathy P.. An integrative transcriptomics approach identifies miR-503 as a candidate master regulator of the estrogen response in MCF-7 breast cancer cells. RNA. 2016; 22:1592–1603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Graveley B.R., Brooks A.N., Carlson J.W., Duff M.O., Landolin J.M., Yang L., Artieri C.G., Baren M.J.V., Boley N., Booth B.W. et al. The developmental transcriptome of Drosophila melanogaster. Nature. 2011; 471:473–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Sykes D.B., Kfoury Y.S., Mercier F.E., Wawer M.J., Law J.M., Haynes M.K., Lewis T.A., Schajnovitz A., Jain E., Lee D. et al. Inhibition of dihydroorotate dehydrogenase overcomes differentiation blockade in acute myeloid leukemia. Cell. 2016; 167:171–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Chu L.-F., Leng N., Zhang J., Hou Z., Mamott D., Vereide D.T., Choi J., Kendziorski C., Stewart R., Thomson J.A.. Single-cell RNA-seq reveals novel regulators of human embryonic stem cell differentiation to definitive endoderm. Genome Biol. 2016; 17:173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Broadbent K.M., Broadbent J.C., Ribacke U., Wirth D., Rinn J.L., Sabeti P.C.. Strand-specific RNA sequencing in Plasmodium falciparum malaria identifies developmentally regulated long non-coding RNA and circular RNA. BMC Genomics. 2015; 16:454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Godec J., Tan Y., Liberzon A., Tamayo P., Bhattacharya S., Butte A.J., Mesirov J.P., Haining W.N.. Compendium of immune signatures identifies conserved and species-specific biology in response to inflammation. Immunity. 2016; 44:194–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. The Gene Ontology Consortium. Gene ontology consortium: going forward. Nucleic Acids Res. 2015; 43:D1049–D1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Nir Yosef A.K., Shalek J.T., Gaublomme H., Jin Y., Lee A., Awasthi C., Wu K., Karwacz S., Xiao M., Jorgolli D. et al. Dynamic regulatory network controlling TH17 cell differentiation. Nature. 2013; 496:461–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Liberzon A., Birger C., Thorvaldsdottir H., Ghandi M., Mesirov J.P., Tamayo P.. The molecular signatures database hallmark gene set collection. Cell Syst. 2015; 1:417–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
ImpulseDE2 is available through Bioconductor and through Github (https://github.com/YosefLab/ImpulseDE2). We made instructions for the usage of DESeq2 with a natural cubic spline basis for temporal data available as Supplementary Data S3.







