Intrinsic circuit organization and theta-gamma oscillation dynamics in the entorhinal cortex of the rat

Animal surgery

Experiments were performed on 39 male Sprague-Dawley rats (250–400g; Hilltop Laboratories), which were anesthetized with urethane (1.5 g/kg, i.p.) and ketamine/xylazine (20 and 2 mg/kg, i.m.). Additional doses of ketamine/xylazine (2 and 0.2 mg/kg) were given as needed. The body temperature was monitored and kept constant with a heating pad. The heart rate, breathing rate and the arterial oxygen saturation were also monitored with an oximeter (MouseOX®, StarrLife Science Corp) during the entire duration of the experiment. The head was placed in a stereotaxic frame, the skull was exposed, and a small hole (1.2 mm in diameter) was drilled above the visual cortex V1 (A, −7.0 mm from the bregma; L, 4.0 mm from the midline; D, 5.0–5.2 mm from brain surface) through which an extracellular recording silicon probe was inserted at a 20° angle caudally in order to target the dorso-medial portion of entorhinal cortex. Another hole was drilled above the ipsilateral visual cortex V2 (A, 9.0; L, 4.0; D, 3.5–4.5 mm from the brain surface) to insert an intracellular electrode vertically close to the extracellular electrode (e.g., Fig. 4A). Two miniature stainless-steel screws were driven into the skull and served as ground and reference electrodes, respectively for extracellular recordings. An Ag-AgCl wire, placed in the neck muscles, served as a reference electrode for intracellular recordings. The skull holes were covered with paraffin-wax mixture after electrode insertion (Henze et al., 2000). All experiments were carried out in accordance with experimental guidelines approved by the Rutgers University Animal Care and Use Committee.

Electrophysiological methods

Extracellular signal was amplified (1000x) and band-pass filtered (1Hz –5 kHz) by a multi-channel AC amplifier (Sensorium EPA5, Sensorium Inc.). The intracellular signals were amplified with a DC amplifier (Axoprobe 1A; Axon Instruments). Wide-band extracellular and intracellular signals were digitized at 20 kHz and stored for offline analysis (64 channels DataMax System, 16-bit resolution, RC Electronics). The extracellular recordings were carried out by either a 4-shank silicon probe (32 sites distributed at 20 μm intervals; NeuroNexus Technologies) placed in EC2-EC3 or EC3-EC5, or a single-shank silicon probe (Acreo) with 32 linearly arranged recording sites (at 50 μm intervals) placed almost perpendicular to the layers of the dorso-medial entorhinal cortex (Figure 4A). On-line positioning of the electrodes was assisted by the presence of unit activity in cell body layers and the reversal of theta (3–6 Hz) oscillations when passing from EC2 to EC1 (Chrobak and Buzsáki, 1998; Mizuseki et al., 2009) and their final positions were confirmed histologically after the experiment. Only experiments with appropriate position of the probe were used for analysis. To facilitate anatomical localization of the track, DiI was applied on the back of the probe shank(s) before insertion.

Intracellular penetrations were carried out with sharp glass capillaries, pulled from borosilicate glass tubes and filled with 1.5 M K-acetate and 2% biocytin (pH 7.4, 40–62 MΩ). After the membrane potential became stable, brief hyperpolarizing and depolarizing current steps were injected through the electrode to characterize membrane potential properties (from −0.5 to 0.5 nA, 500 ms). Only healthy neurons (input resistance >20 MΩ; resting membrane potential <−55 mV and overshooting action potentials) were included for analysis. At the end of the physiological data collection, biocytin was loaded into the recorded neuron by positive current pulses (+0.5 nA, 500 ms at 1 Hz for 5–25 min).

Data analysis

Raw data were preprocessed using a custom-developed suite of programs (Csicsvari et al., 1999). The wide-band signal was down-sampled to 1250 Hz for local field potential signal (LFP) analysis. Single units were isolated from the wide-band signal semi-automatically by a custom-developed clustering analysis program KlustaKwik (http://klustakwik.sourceforge.net/) (Harris et al., 2000) and refined manually using custom-made software (http://klusters.sourceforge.net; http://neuroscope.sourceforge.net; Hazan et al., 2006). Only units showing a clear refractory period and well-defined cluster boundaries were included for analysis. For the separation of putative principal cells and interneurons, we took advantage of the simultaneously recorded cells to assess putative monosynaptic connections among neurons from their cross-correlograms (Barthó et al 2004; Sirota et al 2008; Mizuseki et al 2009). To test for significance of the peaks and troughs in the unit cross-correlograms, a non-parametric significance test, based on jittering of spike trains, was used (Fujisawa et al 2008). In short, the referred point-process dataset was jittered ([−5, +5] ms interval) to produce 1000 surrogate cross-correlograms from which the exact p-value for each time bin was computed over the [−30, +30] ms interval. For each cross-correlogram, global bands at an acceptance level 99% were created from the maximum and minimum of each jitter surrogate cross-correlogram across the interval [−30, +30 msec]. Time bins with p-value of 0.01 or less were considered significant for short latency peaks (or troughs; 1 to 5 msec) in the original cross-correlogram when at least one bin was atypical with respect to the upper (or lower) global band. The significant bin effects were considered to be due to excitation or inhibition of the reference unit by the referred unit (Fujisawa et al., 2008). For cell pairs recorded from the same shank the 0–1 msec bin was not considered because our clustering program cannot resolve superimposed spikes. The cluster properties of the neuron pairs, designated as monosynaptically connected by the statistical analysis, were visually inspected and spurious cell pairs due to potential clustering errors were excluded from further analysis. Using this method, 456 of the 1100 recorded units were classified as excitatory or inhibitory neurons (e.g., Fig. 8). Only this physiologically defined subgroup was included for quantitative analyses. Layer assignment of the neurons was determined from the approximate location of their somata relative to the recordings sites (with the larges amplitude unit corresponding to the putative location of the soma), the known distances between the recording sites and the histological reconstruction of the recording electrode tracks (e.g. Fig. 4A).

Recording sessions were divided into brain states of theta and slow oscillation periods. LFP theta epochs were visually selected from the raw traces, assisted by the ratios of the whitened power in the theta band (3–6 Hz) and the power of the neighboring bands (1–3 Hz and 7–14 Hz) of EC3 LFP (e.g., Fig. 4D). Spectral analyses were carried out using direct multi-taper estimates (Mitra and Pesaran, 1999; Sirota et al 2008). Typically, window sizes of 2–4 seconds and 3–5 tapers were used. The theta phase of the EC3 LFP was determined from the LFP filtered in the theta band (adjusted for the dominant theta frequency in each experiment, typically ~2–6 Hz). The instantaneous phase was computed as the angle of the Hilbert transform and the distribution of the phases in each session was tested for uniformity prior to unit analysis. Using linear interpolation, a value of phase was assigned to each action potential (units and intracellular spikes).

To establish the gamma-phase modulation of units, the gamma bursts in EC3 during theta epochs were detected (Sirota et al., 2008) and the instantaneous phase of gamma oscillation was estimated by Hilbert transform of the 30–90 Hz filtered signal. Only neurons with at least 50 spikes and a firing rate above 0.5 Hz during the theta epochs were included for the LFP-unit analysis. The theta and gamma phase modulation of action potentials was determined by Rayleigh circular statistics (Fisher, 1993); p<0.05 was considered significant. Group comparison tests of circular variables were performed using circular ANOVA.

Coherence between the intracellular membrane potential (V_m) and instantaneous LFP theta was computed using the EC3 LFP signal since recordings from this layer were available in all experiments. For the analyses of V_m fluctuations, the intracellular action potentials (3 msec) were removed and replaced by interpolated values. Spectral power of V_m was computed and the relative power coefficient (ratio of the peak power and the standard deviation across all frequencies) was used to characterize the strength of the dominant frequency of theta oscillation.

The phase and power relationship between V_m and the LFP signal was assessed by spectral methods (Isomura et al., 2006). For the assessment of V_m power - LFP power relationship, the correlation coefficient between normalized spectral power values of the respective signals (V_m and LFP) at all pairs of frequencies was calculated (‘comodugram’).

The magnitude of theta phase-modulation of gamma power (30–90 Hz) and of the high frequencies (> 200 Hz) was estimated by calculating the power of the gamma/fast frequency band in short (50–100 ms) overlapping windows at all the recording sites and correlating the power with the instantaneous phase of theta, obtained from the Hilbert transformation of the filtered signal from EC3 (e.g., Figure 11E).

Current source density (CSD) analysis of the simultaneously recorded field potentials was used to eliminate volume conduction and localize synaptic currents. CSD was computed as the second spatial derivative of the recorded LFPs and smoothed spatially with a triangular kernel (Freeman and Nicholson, 1975). Activity from malfunctioning sites was interpolated from the neighboring sites.

Histological processing

Under deep urethane anesthesia, the animals were perfused intracardially with 100 ml cold saline followed by 250–300 ml of 4% paraformaldehyde in 0.1M phosphate-buffer (PB, pH=7.4). The brains were removed and postfixed at 4°C overnight. They were then rinsed in PBS, cryoprotected in 20% sucrose in PB for 24h and quickly frozen on dry ice. The brains were sliced into 40-μm-thick parasaggital sections by a Vibratome (Leica). The biocytin-loaded neurons were labeled in serial sections by the avidin-biotin-HRP complex (Vector Laboratories) method. The sections were mounted on gelatin-coated glass slides and counter-stained with thionin (Fig. 2). The labeled neurons were reconstructed from multiple serial sections with NeuroLucida (MicroBrightField Inc.), together with the tracks of the extracellular silicon probes. In each section, the processes (dendrites and/or axons) were traced taking into account their depth in the section. In addition, the contours of the cortical layers were outlined (Fig. 1). The NeuroLucida software was used to quantify the length and pattern of the dendritic and axonal processes in the three dimensions. For each cell, the total number of boutons was estimated from a partial count of boutons over a 200 to 600 μm axon segment in each layer, using a 100x oil-immersed objective. The bouton density was calculated as the number of boutons per 100 μm axonal segment. All measurements were corrected for an estimated 20% tissue shrinkage.

Dendritic and axonal arborization of EC principal neurons

We have obtained stable intracellular recordings from 8 layer II (EC2), 15 layer III (EC3) and 12 layer V (EC5) histologically verified neurons of the dorso-medial entorhinal cortex (EC). The soma size, dendritic morphology and layer distribution of dendritic branches were similar to those described previously in both in vitro and in vivo (supplemental Table 1; supplemental Fig. 1; Germroth et al., 1989; Klink and Alonso, 1997; Dickson et al. 2000; Tamamaki and Nojyo 1993; Alonso and Klink 1993; van der Linden and Lopes da Silva 1998; Lingenhöhl and Finch 1991). Therefore, our description of the neurons focuses mainly on their 3-dimensional axon arborization within the EC. For detailed anatomical analyses, we have chosen two EC2, two EC3 and an EC5 cell on the basis of their extensive axonal arborizations.

Theta oscillations in EC neurons

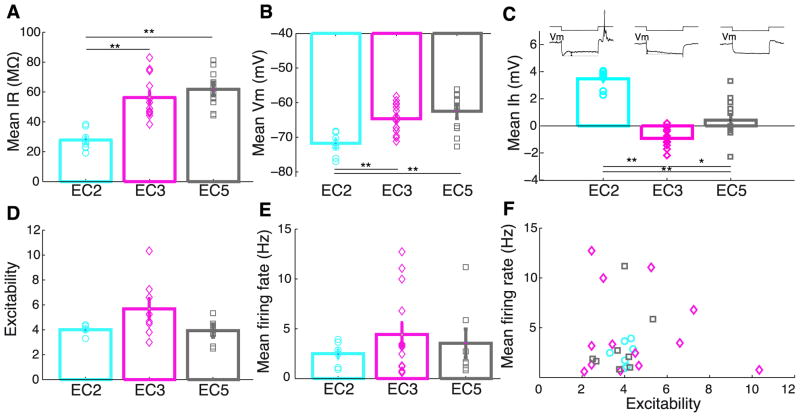
EC2 stellate cells had a significantly lower input resistance (P<10⁻⁴ and P<10⁻⁶ vs. EC3 and EC5 respectively; ANOVA test) and were significantly more hyperpolarized (Fig. 3A and B; P<10⁻³ and P<10⁻³, respectively) than EC3 and EC5 cells. In addition, EC2 but not EC3 and EC5 neurons (Dickson et al., 1997), had a prominent depolarizing ‘sag’ (I_h; Alonso and Llinas, 1989; Dickson et al., 2000) in response to hyperpolarizing current steps (Fig. 3C). In contrast to EC2 stellate cells, EC3 neurons did not show a sag but, instead, an enhanced slow hyperpolarizing response to hyperpolarizing steps (Fig. 3C, top inset). This conductance may explain why EC3 pyramidal cells took significantly longer time to latch back from the ‘UP’ to the ‘DOWN’ state during slow oscillations than other EC principal cells (Isomura et al., 2006). In response to depolarizing pulses (0.5 nA), neurons in all layers fired approximately the same number of spikes (4–5 spikes/500 msec pulses; Fig. 3D). Some neurons fired with bursts, others with relatively regular spikes but no obvious firing pattern differences were detected across the three groups (but see firing pattern differences in the waking animal; Mizuseki et al., 2009). The spontaneous firing rates, computed from theta epochs of the entire recording session, were comparable between the neuron groups (Fig. 3E). No reliable relationship was found between spontaneous firing rate and current induced excitability (Fig. 3F) or between rate and input resistance, suggesting that firing rates are mainly determined by the network into which the neurons are embedded rather than by their biophysical properties.

The network-related behavior of the three groups was markedly different. The simultaneously recorded extracellular LFP, spanning several layers of the EC by the silicon probe, allowed for an unequivocal classification of the epochs into theta or slow oscillations (Fig. 4). These network patterns alternated spontaneously or the state change was induced by pinching the tail of the rat or by an additional dose of the anesthetic. In the absence of theta oscillations, several EC neurons showed a prominent slow oscillation (0.5–1.5 Hz), consisting of alternating depolarized UP states with spikes and hyperpolarized DOWN states (Fig. 4). The voltage difference between UP and DOWN states was significantly smaller in EC2 stellate cells than in EC3 and EC5 neurons (P<0.005; ANOVA). Although the voltage distribution in both EC3 and EC5 neurons was prominently bimodal, the UP to DOWN transition was slower in EC3, perhaps due to the slow hyperpolarizing response of the membrane in these cells (Fig. 3C; see also Isomura et al., 2006). In contrast, during theta oscillations the membrane voltage distribution was unimodal in all neurons but the magnitude of theta-related voltage fluctuation was significantly larger in EC2 stellate neurons than in EC3 and EC5 pyramidal cells (P<0.002; Fig. 5).

Because LFP is generated by the integrated electric dipole moments of the membrane currents of neurons (Buzsáki et al., 2003; Nunez and Srinivasan, 2006), examination of the relationship between LFP and concurrently recorded V_m in identified single neurons can provide information about their contribution to the LFP (Stewart et al., 1992). For these analyses, the action potentials were removed from the intracellular recordings and the missing bins were interpolated (see Experimental Procedures; Isomura et al., 2006). Figure 5A illustrates the activity of representative neurons in each EC layer during theta oscillation. The magnitude of theta-related V_m varied from 0.2 to 6 mV in different cells. EC2 stellate cells showed the largest amplitude and most coherent membrane potential oscillations with the extracellular LFP theta. The LFP-normalized intracellular theta power was significantly larger in EC2 than in EC3 and EC5 cells (Fig. 5C; P<0.002; ANOVA test). As expected, the intracellular and LFP theta power were correlated (Fig. 5D; P<0.04 THESE SHOULD BE P VALUES, AT LEAST THIS IS WHAT I GOT FROM YOU; R2 VALUES SO LOW WOULD NOT MAKE ANY SENSE). In the EC2 group, the LFP theta power negatively correlated with the mean membrane voltage (V_m) of the neurons (Fig. 5E; P<0.04; EC2 differed significantly from EC5 group; P<0.05; MANOVA). The strongest LFP-intracellular V_m coherence was present in EC2 stellate cells (Fig. 5F). The magnitude of the coherence was correlated with the intracellular theta power (P<0.05 for EC2 and P<10⁻³ for all cells R2 VALUES SO LOW WOULD NOT MAKE ANY SENSE!!) but was independent of the LFP theta power or its frequency (Fig. 5G–I).

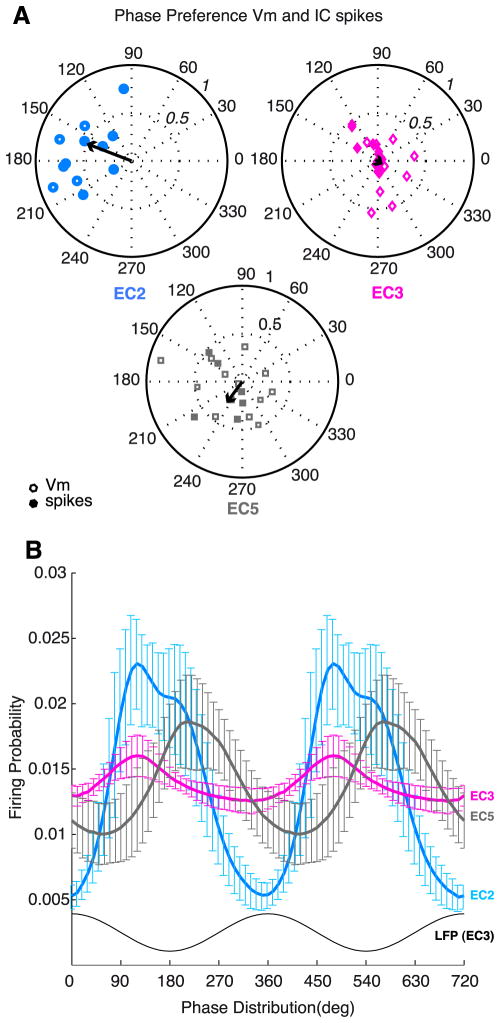
In addition to the magnitude of intracellular theta and its coherence to LFP in single neurons, the magnitude of the extracellular current flow also depends on the temporally coherent fluctuation of V_m across neurons (Buzsáki et al., 2003; Logothethis, 2003; Nunez and Srinivasan, 2006). Therefore, we also examined the phase-preference of the intracellularly recorded neurons to LFP theta, using 3 complementary measures: the distribution of the phase difference between LFP and intracellular (V_m) theta oscillations in single cells, the distribution of preferred phases of single neuron spikes and theta phase distribution of all spikes in all cells. The 3 approaches gave similar results (Fig. 6). Both the intracellular theta (V_m) and spike preference of single EC2 neurons showed a relatively narrow phase distribution, close to the trough of EC3 LFP theta. In contrast, neurons in both EC3 and EC5 had a large variability of phase preference (Fig. 6A). Accordingly, the spikes of the EC2 population showed a strong theta modulation with the maximum spiking near the trough of EC3 theta (Fig. 6B). Neurons in the EC3 group were least theta-modulated, whereas EC5 cells occupied an intermediate position (Fig. 6B).

In summary, EC2 stellate neurons showed distinct biophysical properties from other EC neurons and displayed largest amplitude V_m oscillations during theta activity. Furthermore, EC2 stellate cells fired consistently phase-locked to the trough of the EC3 LFP theta, whereas the phase preference and theta-entrainment of EC3 and EC5 pyramidal cells were more variable.

Depth profiles of theta, gamma and high frequency power

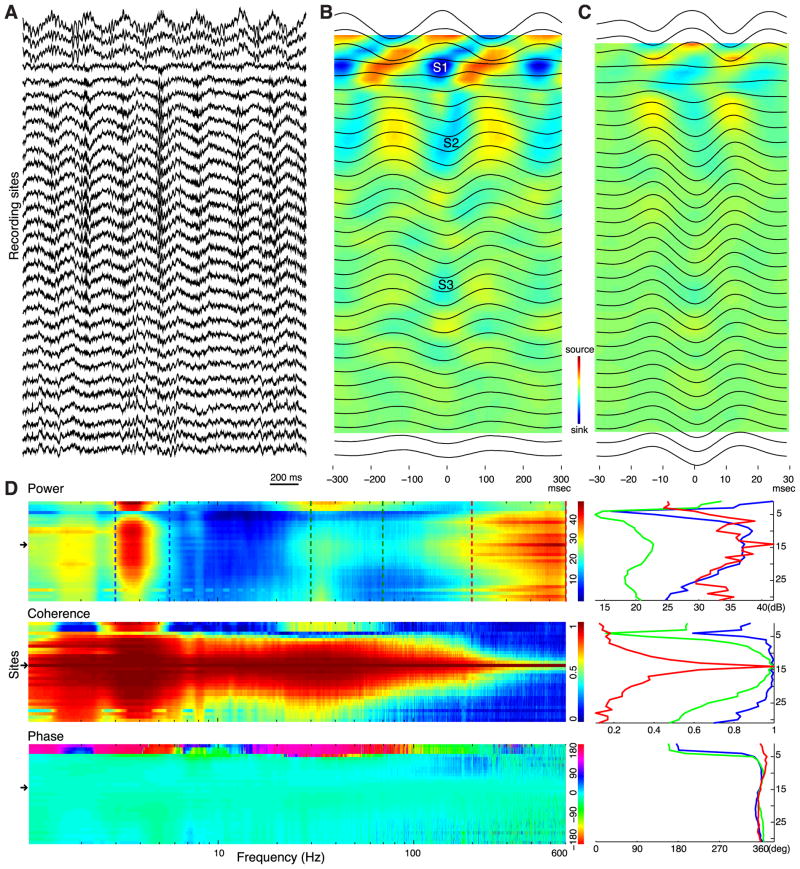
Extracellular LFP was monitored by multiple-site silicon probes. In experiments using the single-shank 32-site probe, depth distribution of the various LFP pattern could be studied quantitatively (Fig. 7). The paucity of unit firing at the most superficial sites identified EC1, with a large increase of spiking activity in EC2. The location of the EC1-EC2 border and the histologically verified track of the probe allowed us to estimate the border between EC3 and EC5. In agreement with previous experiments (Alonso and Garcia-Austt, 1987a; Mitchell and Ranck, 1980; Chrobak and Buzsáki, 1998; Cunningham et al., 2003; Hafting et al., 2008), we found a large dip of both theta (3–5 Hz) and gamma (30–60 Hz) power and coherence, relative to the EC3 reference site, and a phase reversal of both theta and gamma rhythms between EC1 and EC2 (Fig. 7A–D). Both theta and gamma LFP were in phase in EC2 to EC5 and highly coherent within EC3. The phase of gamma waves reversed at nearly the same depth as the phase-reversal of theta oscillations (Fig. 7B, C).

In addition to theta and gamma rhythms, the whitened power spectrum also showed a broad ‘peak’ above 100 Hz (Cunningham et al., 2004; Canolty et al., 2006; Sirota et al., 2008; Colgin et al., 2009). The absolute power of this high frequency band was only a small fraction of the theta and gamma power, and had a relatively uniform power distribution between 150 Hz and 3 kHz. The depth distribution of the high frequency power was associated with the presence of unit spiking, with very low power in EC1 and highest power at sites with strong unit activity (see also Cunningham et al., 2004). This high frequency activity was spatially confined as was evidenced by the fast decrease of coherence values with distance (Fig. 7D), independent of the chosen reference site. The spatial extent of the coherence in the high frequency band corresponded to the span of the extracellularly recordable action potentials from the same neurons (Henze et al., 2000). These findings suggest that the high frequency pattern largely reflects spectral properties of action potentials, most likely summed spike afterpotentials, rather than genuine oscillations.

Current source density (CSD) analysis of theta oscillations revealed a strong sink in the deeper part of EC1 (S1 in Fig. 7B) and weaker sinks in the superficial and deeper parts of EC3 (S2 and S3 in Fig. 7B). The strongest sink in EC1 is an indication of inward current, possibly induced by the recurrent collaterals of EC2 neurons terminating on the apical dendrites of EC cells. The origin of S2 and S3 is less clear since their magnitude and position showed more variability across different experiments (supplemental Fig. 3). As expected from the power and phase depth profiles of gamma oscillations, the largest sink-source pair of gamma was present at the EC1-EC2 border, with only weak additional sinks in deeper layers. These observations suggest that although all principal cell type participates in the generation of LFP theta, EC2 neurons provide the strongest theta dipoles.

Theta phase-modulation of extracellularly recorded neurons

The layer identity of the extracellularly recorded neurons was assisted by the layer-specific LFP patterns (Mizuseki et al., 2009). Units recorded at the border of layers with ambiguous layer identity were discarded. Since we could not routinely distinguish between EC5 and EC6 layers with our methods, they were lumped together as EC5. Extracellularly recorded neurons contain both principal cells and interneurons. Because the intracellularly recorded and identified neurons revealed large variations in the firing rates and autocorrelogram patterns even within the same group (supplemental Fig. 3), and because previous works indicated that these parameters are not reliable predictors of neuron type identity in the EC (Mizuseki et al., 2009), we took advantage of the simultaneously recorded EC cells to identify the recorded units as excitatory or inhibitory neurons by their short-latency temporal interactions with other neurons (Barthó et al., 2004; Sirota et al., 2008; Mizuseki et al., 2009). Putative monosynaptic connections were associated with precisely timed spiking relationships at short (<5 ms) latency offsets between two recorded neurons, as illustrated by the narrow, short-latency peak or trough in the cross-correlogram (Fig. 8A, B; Mizuseki et al., 2009). We also found inhibitory connections between putative interneuron-intracellularly recorded cell pairs (n=2), with mean unitary IPSPs of ~ 0.1 mV (Fig. 8C). The time course of the IPSP, superimposed on the large theta-associated V_m, corresponded to the time course of spike suppression. These putative monosynaptic connections allowed the reconstruction of functional subnetworks in different layers of the EC (Fig. 8E). In two experiments, we found putative excitatory connections between excitatory EC2 neurons (a pair is shown in Fig. 8E; pair 1 and 2). While we did not find excitatory monosynaptic connections between intracellularly identified neurons and extracellularly recorded units (but see Marshall et al., 2002), current-induced action potentials in two neurons reliably altered local network activity, as reflected by the complex, multisynaptic effects they evoked (Fig. 8F; Szabadics et al., 2006).

Using the above criteria, we identified 196 putative principal cells and 260 interneurons from the total of 1100 unit clusters and used them for further analysis. Note that the cross-correlation identification method is biased in favor of finding more inhibitory interneurons because of the stronger connections between interneurons and principal cells than among principal cells (Barthó et al., 2004).

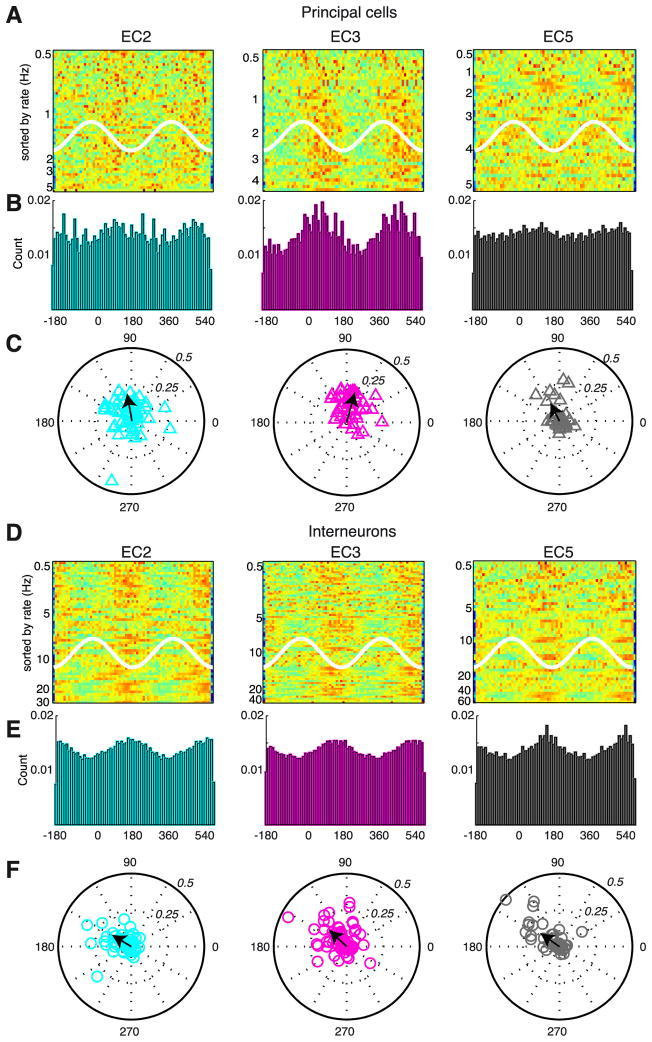
To examine the spike-theta phase relationship of extracellularly recorded neurons, we used two complementary measures: the distribution of preferred phases of single neurons (Fig. 9A, C, D, F) and theta phase distribution of all the spikes in the population (Fig. 9B, E). As in the waking rat (Chrobak and Buzsáki, 1998; Hafting et al., 2008; Mizuseki et al., 2009), EC2 neurons showed strong phase-locking to the trough of EC3 LFP theta (Stewart et al., 1992) and contained the highest fraction of significantly theta modulated neurons (Fig. 9A–D). In contrast, the EC3 principal cell group contained only a small fraction of significantly modulated cells and individual EC3 principal cells showed a wide range of theta phase preferences. As a result, the putative EC3 principal cells were least modulated by the theta cycle as a population. The EC2 and EC3 populations fired on the opposite phases of theta (Fig. 9B–C). Phase preference of putative EC 5 principal cells was also variable (Chrobak and Buzsáki, 1994; 1998; Frank et al., 2001; Mizuseki et al., 2009). This situation is different from the waking animal, where EC3 neurons fire coherently on the same phase of theta, whereas EC2 principal cells have an activity-dependent distribution on a wide range of phases (Mizuseki et al., 2009). These firing patterns differences may contribute to the different depth profiles of theta oscillations in the hippocampus in waking and anesthetized rats (supplemental Fig. 2). The physiologically identified inhibitory interneuron groups in all layers tended to fire at the same phase (near the EC3 theta trough and on the ascending phase), with the EC2 group showing the strongest theta modulation (Fig. 9D–F; P<0.005; ANOVA) and were silenced together at approximately the same theta phase. In EC5, a minority of relatively well-modulated interneurons fired at either the trough or on the ascending phase. In summary, the extracellulary recorded units in various EC layers showed similar phase preference and proportionally similar magnitude of theta modulation as the intracellularly identified subsets of EC2, EC3 and EC5 neurons.

Gamma modulation of EC neurons

To study the contribution of various neuron types to gamma oscillations, the wide-band trace was band-pass filtered (30–90 Hz) and the troughs of the gamma waves were detected. Spikes were referenced to the phase of local gamma detected by the adjacent electrode site on the same shank. EC3 principal cells showed the strongest phase-locking to the descending phase of the local LFP gamma, followed by EC2 and EC5 principal cells (Fig. 10A–C). Interneurons in EC2, EC3 and EC5 showed approximately the same magnitude of gamma phase modulation and lagged 45° to 60° after the respective principal cell population (Fig. 10D–F). Gamma phase-locking of units in different layers, referenced to a common EC3 LFP gamma, is shown in supplemental Figure 4.

The magnitude of intracellular gamma-associated V_m change was small relative to theta V_m oscillations in all cases (30 μV to 300 μV; Fig. 11A). Gamma power of V_m with a distinct peak was observed in only in two EC2 and two EC3 neurons (an example is shown Figure 11B, arrow). To improve the gamma-to-noise ratio in V_m, we generated spike-triggered averages of V_m, triggered by the physiologically identified inhibitory neurons (Matsumura et al., 1996). These spike triggered-V_m averages revealed IPSPs superimposed on the intracellular theta signal and time-locked to the spikes of the putative interneurons (Fig. 11D). The intervals of the IPSPs (20–40 msec) corresponded to the mean frequency of the simultaneously recorded LFP gamma (arrows in Fig. 11D).

Theta phase-modulation of gamma and high-frequency power

The co-modulation of theta and gamma power is illustrated in Figure 10C (arrow). The power of both gamma oscillations and the high frequency band was modulated by the phase of theta oscillations in each layer (Fig. 11E, F). The theta phase relationship of gamma power (30–90 Hz) allowed for further separation of EC1-2 and deeper layer gamma oscillations. Gamma power in the superficial layers was largest right after the EC3 theta peak, whereas EC3 gamma power was maximal on the late descending part. In all layers, including EC5, gamma power had a minimum on the ascending phase of EC3 theta (Fig. 11E), coinciding with the phase of least interneuronal activity (Fig. 10D–F). In contrast, the high-frequency power was locked to the trough of EC3 theta (Fig. 11F), where most spiking activity was present (Fig. 9 and 10). These findings indicate that, similar to the hippocampus (Bragin et al., 1995; Csicsvari et al., 2008; Montgomery et al., 2007), gamma oscillations can be generated locally in each EC layer and that these oscillations are coordinated by the phase of hippocampal theta rhythm (Chrobak and Buzsáki, 1998).

Connectivity of the principal cells in the EC

Although the number of intracellularly labeled neurons in our study was limited, certain tentative conclusions from their axonal arbors can be made. EC5 neurons may contribute 3- and 5-times more intrinsic connections than EC2 and EC3 neurons, respectively. Both EC5 and EC2 neuron have extensive connections in both medio-lateral and fronto-caudal directions (Dolorfo and Amaral, 1998a, b; Lingenhohl and Finch, 1991; Jones 1994; Gloveli et al., 2001; Kink and Alonso, 1997; Tamamaki and Nojyo, 1993; Hamam et al., 2000; Amaral and Alonso, 2002), whereas axon collaterals of EC3 neurons are more restricted spatially (Gemroth et al., 1989; Lingenhohl and Finch, 1991). EC5 neurons form a cone-shape axon arbor with its base in EC5 and its peak in EC2. This arrangement suggests that EC5 cells communicate mainly with their peers within the same layer through the basal dendrites and with progressively fewer neurons in EC3 toward the surface, contributing few axons to EC2-EC1 (van Haeften et al., 2003; Kloosterman et al., 2003; 2004). The axon cloud of EC2 stellate cells is an inverted cone with its wide base in EC1 and peak at the EC3-EC5 border. Assuming that connectivity follows the distribution of the available target neurons, the broad and dense axon collaterals of EC2 stellate cells in EC1 indicates that they form connections with the apical dendrites of both superficial and deep layer principal cells in a wide cylinder. Therefore, EC2 stellate cells can address a wide array of EC2, EC3 and EC5 neurons. The divergent-convergent EC2-EC3-EC2 recurrent loop may be instrumental in segregating neurons both spatially and temporally. In contrast, EC5 pyramidal cells would influence only very few superficial neurons directly, indicating a strongly asymmetric divergent-convergent communication between EC2 and EC5 principal cells. The axons of EC3 cells form a relatively narrow barrel with most axon terminals ending in EC3 and progressively less in deeper and more superficial layers (Gemroth et al., 1979; Lingenhohl and Finch, 1991). Such distribution of axon collaterals suggests that EC3 neurons provide the critical bidirectional conduit between superficial and deep layers so that the inputs from both EC2 and EC5 can activate many EC3 neurons, whereas the EC3 outputs converge on smaller subsets of EC2 and/or EC5 cells, restricting the spatial spread of excitatory activity from deep to superficial layers (Kloosterman et al., 2003; 2004). Embedded in this excitatory web reside a variety of interneuron families, whose connectivity is poorly understood. Furthermore, there might be variations of connectivity within each layer, adding more computational power to the circuits (Canto et al., 2008).

The special architecture of the EC must have important implications for its functional operations. Generation of the grid pattern in EC2 neurons is believed to be dependent on attractor dynamics supported by recurrent networks (McNaughton et al., 2006; Burgess et al., 2007; Hasselmo et al., 2007; Hasselmo, 2008). Our findings support the existence the postulated recurrent networks EC2. EC2 neurons had very extensive axon collaterals in EC1, presumably contacting dendrites of principal cells of all layers. Although this claim should be supported by future electronmicroscopic data, the presence of recurrent connections is supported by our physiological evidence, showing monosynaptic connections between pairs of putative EC2 principal neurons. The lack of physiological connections between pairs of EC2 neurons in a previous study (Dhillon and Jones, 2000) could be explained by the strongly reduced axonal arborization in the slice preparation (Menno Witter, personal communication). The postulated recurrent connections among EC5 neurons are supported by previous experiments (Lingenhohl and Finch, 1991; Jones 1994).

Theta oscillations in the EC

Although the current experiments were carried out under anesthesia (see discussion of caveats in supplemental Fig. 2), a number of observations indicate the critical role of the EC circuits in theta oscillations. First, stellate cells are endowed with intrinsic properties that facilitates oscillation at theta frequency (Alonso and Llinas, 1989; Klink and Alonso, 1997; Dickson et al 2000). A prominent ‘sag’ (HCN-1 channel-mediated h current; Alonso and Llinas, 1989; Giocomo et al., 2007) was present in all of the intracellularly recorded EC2 neurons but absent in other principal cells. Second, EC2 stellate cells showed the largest theta power and most coherent V_m oscillations with the extracellular LFP theta of all EC neurons. The low input impedance, coupled with large amplitude theta-associated V_m change in EC2 neurons, compared to EC3 and EC5 cells, implies a strong theta-associated membrane currents in stellate cells, and hence several times larger contribution to the LFP theta than that of the other EC neurons. The theta behavior of V_m in EC cells can be contrasted to their activity during slow oscillations when the V_m of EC3 and EC5 neurons show prominent bimodality in phase with the LFP slow oscillation, while EC2 stellate cells rarely do so (Isomura et al., 2006). These observations suggest that the intrinsic properties of EC2 stellate neurons are tuned to resonate at theta frequency (Giocomo et al; 2007; Giocomo and Hasselmo, 2008). Third, EC2 stellate cells, as a group, behaved coherently, as shown by the narrow phase distribution of both V_m and spike preference of single EC2 neurons during theta oscillation. In contrast, pyramidal cells in both EC3 and EC5 had a large variability of theta phase preference. Finally, theta amplitude was largest in EC1, a layer to which EC2 neurons contribute the most axon collaterals and boutons.

The largest amplitude theta waves in EC1, the layer containing the distal apical dendritic arbor of EC principal cells, are reminiscent of the similarly largest theta power in the CA1 str. lacunosum-moleculare (Kamondi et al., 1998). The phase reversal of theta waves above the cell bodies of EC2 cells, again similar to CA1 pyramidal cells (Winson 1974), can be explained by inhibitory sources on the large cell bodies of EC2 stellate neurons. Voltage-gated Ca²⁺ spikes in the apical tufts of EC2 and/or EC3-EC5 neurons can further amplify the synapse-mediated sinks in EC1, similar to the distal dendrites of CA1 pyramidal neurons (Kamondi et al., 1998). Overall, the dedicated theta generation mechanisms and special loop connectivity (putative EC2-EC2; E2-EC3-EC2) lend support to the hypothesized mechanisms underlying grid pattern formation in EC2 cells (Samsonovich and McNaughton, 1997; McNaughton et al., 2006; Fuhs and Touretzky, 2006; Moser and Moser, 2008).

Gamma oscillations in the EC

Gamma oscillations in the EC and their interactions with hippocampal gamma (Charpak et al., 1995; Chrobak and Buzsáki, 1998; Colgin et al., 2009) are assumed to support basic operations at the EC-hippocampal interface, including learning and memory (Fell et al., 2001; 2002; Steinvorth et al., 2009). Gamma oscillations in the EC may arise from multiple mechanisms (Cunnigham et al., 2003, 2004, 2006; Middleton et al., 2008). In agreement with in vitro studies (Cunningham et al., 2003; Middleton et al., 2008), we found that gamma oscillations independently emerged in different layers. The largest amplitude gamma oscillations were observed in EC1-EC2, with a null zone and abrupt phase-reversal between EC1 and EC2 (Chrobak et al., 1998). The absence of well-defined gamma dipoles in the other layers may be due to the extensive vertical dispersion of principal cell bodies and the temporal variation of short-lasting gamma bursts in the various layers (Sirota et al., 2008). The distinct nature of layer-specific gamma oscillations was also demonstrated by the theta phase-modulation of gamma power, with EC2 gamma power peaking on the descending theta phase, followed by EC3 and EC5 gamma oscillations at later phases. The spatial and temporal segregation of EC gamma rhythms may engage different regions of the hippocampus in a task-specific manner (Charpak et al., 1995; Chrobak and Buzsáki, 1998; Middleton et al., 2008; Colgin et al., 2009).

Overall, maximum gamma power coincided with the descending phase of EC3 theta and preceded the maximum discharge of the principal cells. It is notable that a similar phase relationship exists in the hippocampal CA1 region (Bragin et al., 1995; Buzsáki et al., 2003), implying a general mechanism. The temporal delay between gamma power maximum and the maximum probability of spiking may serve two purposes. First, the gamma-related hyperpolarization of the V_m may effectively lower the spike threshold by erasing the spiking history-dependent reduction of the available Na⁺ channels (Spruston et al., 1995; Henze and Buzsáki, 2001). Second, the release of the V_m from transient hyperpolarization can facilitate ‘rebound’ spiking (Cobb et al., 1995), which may be particularly effective in neurons with prominent I_h (Alonso and Klink 1993; Giocomo et al., 2007). How the different EC gamma generators interact with layer-specific gamma rhythms in the hippocampus and serve various aspects of behavior remains a challenge for future experiments.